基于动态变粒度的改进基态修正模型研究

姚茂华　周文婷

[摘要]分析基态修正模型的特点和研究进展,提出基于动态变粒度的改进基态修正模型,该模型引入动态变粒度基态距因子来确定基态距阀值,是对基态修正模型进行进一步改进,提高历史数据的存储和检索效率;针对该改进基态修正模型,分析时空数据的检索方式,实现多种方案的时空数据检索。

[关键词]时态GIS 时空数据模型 基态修正 时空数据检索

中图分类号:TP3文献标识码:A文章编号:1671-7597(2009)0910043-03

一、引言

由于时间是反映地理实体的状态和演变过程的重要组成部分,任何地理实体都有其产生、发展和灭亡的时间过程,因此,在描述地理实体的空间和属性特征的同时,也必须描述它具体的存在时间,才能反映客观真实世界。能够处理时间信息的时态地理信息系统(Temporal Geogaphical Information System,简称TGIS)就成为GIS研究的热点。

TGIS的关键问题是建立合适的时空数据模型,许多学者提出了多种时空数据模型来存储时态数据,主要包括:序列快照模型、基态修正模型、时空复合模型、第一范式时空数据模型、非第一范式时空数据模型、基于事件的时空数据模型等。其中,基态修正模型不存储研究区域内的每个时刻的全部信息,只存储某个时刻的全部信息(基态)以及其他时刻相对于基态时刻的信息变化量,得到了越来越广泛的关注[1]。

二、基态修正模型特点

基态修正模型是Peuquek和Duan于1995年提出的[2]。基态修正模型按事先设定的时间间隔采样,只储存某个时刻的数据状态(称基态)和相对于基态的变化量。由于对于每一次变化,基态修正模型仅记录变化的增量,只有很小的数据量需记录,因此数据冗余较少,而且也能充分地表达地物的变化情况。然而,在对某一历史时刻查询的时候需要按顺序进行数据叠加操作,整合出一套完整的空间数据,当时间比较久远、变化次数较多时,对历史数据的检索时间较长,查询的效率会非常低。如何减少数据冗余、高效地进行查询和分析,已经成为许多学者研究的问题[3-5]。

三、基态修正模型的改进方法

针对传统的基态修正模型对历史数据的检索时间长的问题,研究基态修正模型的学者对于传统的基态修正模型进行改进和扩展主要围绕如何更科学的设置基态和快速索引展开。张祖勋等(1996)提出了建立多级差文件的方法减少历史数据恢复时检索差文件的个数[6];曹志月(2002)等人认为当历史久远时建立多级差文件方法仍不理想,提出了多基态修正法,提高检索的速度[7];刘仁义等(2002)认为时态数据库用户对数据具有厚今薄古或对某一特定时期操作频繁的特点,提出了双基态/多基态修正,并在理论探讨的基础上,进一步采用区段快速索引和变粒度存储技术提高了时态查询效率[8];余志文等(2003)提出了面向对象方法的基态修正模型以及基态距因子与等比系数方法等;张保钢(2005)认为当历史久远时,基态的占用空间仍是非常可观的,提出了多基态多级差文件修正方法[9];李勇(2005)以对象变化临界指数确定基态距的方法[10],改进基态修正时空数据模型。现在修正模型的理论与技术两方面发展相对较为成熟,且已在土地、房产等相关领域的TGIS系统中得到应用。

总结基态修正时空数据模型的存储方式及其改进方法,主要有以下几种比较典型的基态修正方式[11]。

图1(a)是Langran[12]的基态修正方式,只记录了一个数据基态和相对于基态的变化值,这种方式在发生变化的对象数量很多时,由于关系表中存储了太多的历史数据,因而对历史数据进行检索时速度很慢,查询效率很低。

图1(b)是张祖勋等[6]改进后的基态修正方式。他们把时间段T分成两部分,对前半段时间,从起始状态不断阅读差文件,状态不断沿着时间轴正向变化,直到查询到所需时刻为止;而对后半段时间,从现在状态不断阅读差文件,状态不断沿着时间轴反向变化,直到查询到所需时刻为止。这种方式同样有其不足之处:将时间段T分成两部分只是临时性地解决检索时历史数据过多的问题,当时间段T进一步延长时(比如当T延长到2倍时),此方法实际上就没有任何意义了。

图1(c)是曹志月等人提出动态多级索引方法[7],在整个历史状态中动态地设立多个基态,基态间的差文件数,称为基态距(k)。系统中,随着对象历史状态的插入、修正,以及对历史时期的检索频繁程度而动态地创立基态。当用户对某时间段的检索较频繁时,特别是对于连续变化的时空过程,差文件的恢复中大量的连续变化属性的推导过程会占去较大的时间开销,通过动态创建差文件和基态的方法,缓解了这一问题,动态多级索引方法大大提高了查询效率。但是,基态距k是等距的,基态的分布位置不是最优的基态位置。

图1(d)和图1(e)是张宝钢等在曹志月等人提出的动态多级索引方法的基础上增加单级和多级时间索引,提出的多基态多级差文件修正方法[9],该方法中,基态仍以快照方式存储,基态数没有增加,每两个基态之间增加了3个的差文件,数据的存储空间基本没有增加,数据检索的速度却有很大的提高。然而,当基态距较小时或是历史较久远时,基态个数会随之增加,也就意味着较大的数据冗余。

图1(f)是余志文等[11]根据变粒度基态距因子理论提出修正方式。其基本思想是:各个历史时期查询的频繁程度是不同的,离现在时刻越远的历史时期,查询的频繁程度越小;离现在时刻越近的历史时期,查询的频繁程度越大。因此,引入变粒度基态距因子,离现在时刻越远的基态之间的基态距越大,离现在时刻越近的基态之间的基态距越小。但是,对于在短时间内数据变化频繁的情况下,基态距与时间的相关性会减弱。

图1(g)是李勇[10]提出根据“对象变化临界指数(M)”来确定基态距的基态修正方式。其基本思路为:①造成数据检索时间长的根本原因是数据量。②事物的变化都是一个从“量变到质变”的过程,而在这个过程中,总会有一个临界点,当达到或超过这个临界点时,就会发生质变。因此,两个相邻基态之间的基态距既不是等距的,也不是随时间的迫近而递减的,而是根据对象发生变化是否达到或超过对象变化临界指数(M)来确定的。这里的关键问题是M值如何确定,其中,相邻两个基态的前一个基态的数据量是决定因子之一,还有就是相邻两个基态之间对象发生变化的次数,发生变化的次数越多,数据库中增加的记录就越多。但是,影响M取值的因子很多,确定比较困难。

四、动态变粒度的改进基态修正模型

基态修正模型减少数据冗余的秘诀在于在对象发生变更时,只存储该时刻的变化量(差文件),而不存储该时刻所有数据以避免重复存储,但是随着变化的频度和力度的加大,会增加差文件的数量,因此进行历史回顾时,必须依赖该时刻与当前时刻间的各个差文件和当前基态进行逐步回退求解,这个计算量随着时间的推移和变化的加快会成倍增长。为了使历史回溯检索的时间缩短,需要建立新的基态,作为此段时间的检索起点,缩短对较远的历史数据的查询时间,其中一个关键的问题是基态距阀值的确定。有些改进的基态修正模型随时间的发展不断增加基态的占用空间,降低检索时间的开销,因此,基态距阀值的确定需要对这两方面进行权衡,阀值太小会浪费空间,阀值太大又会占用过多时间。如果根据数据变化数量和查询频率确定基态距阀值,适当地在对象发生变化的过程中记录若干个基态,则不会造成太多的数据冗余,并可提高历史回顾的效率。

动态变粒度的改进基态修正模型就是基于上述思想设计的时空数据存储模型(如图2所示)。对象发生变化,就会有相应于上一次变化的差文件产生,基态距是两个基态间的差文件数,两个相邻基态之间的基态距不是等距的,需要动态变化,动态地建立基态,只有与查询频率分布和变化数量分布相符合的基态分布位置才是最好的基态位置。各个历史时期查询的频繁程度是不同的,离现在时刻越远的历史时期,查询的频繁程度越小;离现在时刻越近的历史时期,查询的频繁程度越大。不同时间段的数据变化更新数量直接影响差文件数,变化次数越多,差文件越多,查询的等待时间越长,反之则越短。因此,影响基态距的因子有:数据变化数量和离现在时刻的远近。

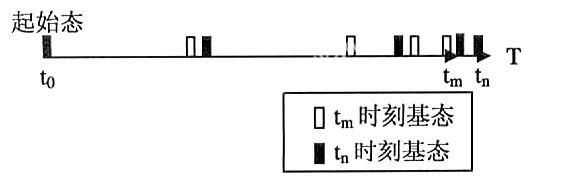
因此,引入动态变粒度基态距因子,数据变化更新数量和离现在时刻的远近决定基态距阀值。除了起始基态外,其余的基态都要随着时间的不断前移而每隔一段时间进行自动更新。基态距是根据对象发生变化是否达到变化阀值Q确定的。

在分析影响基态距的因子后,引入系数a(a≠1),设ti时刻距现在时刻的时间差为△ti,在△ti时间内的差文件数为qi,基态距阀值为Qi,则Qi=a×△ti。当在△ti时间内,变化差文件数qi大于或等于基态距阀值Qi时(即qi≥Qi),需要产生基态,如图2所示。时间差△ti越小,基态距阀值Qi越小;时间差△ti越大,变化基态距阀值Qi越大。设起始状态距现在时刻的时间差为△t0,变化差文件数为q0,即为总差文件数,也是基态距阀值Q0(Q0=q0),由Q0=a×△t0,则可确定系数a。

当△ti较小时,即离现在时刻很近时,若变化差文件数qi小于基态距阀值Qi,则在该时刻不设立基态;当△ti较大时,即离现在时刻很远时,若变化差文件数qi小于基态距阀值Qi,则在该时刻也不设立基态。

随着时间的推移,基态距阀值逐渐变大,通过上述公式,可以求出新基态所在的差文件位置,旧基态加上新旧基态时间段内的差文件,即可更新为新基态。

动态变粒度的改进基态修正模型在整个时间过程中,随着时间的推进和对象的变化,考虑了数据的变化数量和数据的查询频率对数据查询效率的影响,根据对象变化是否达到变化阀值Qi,动态地创建基态,使得对对象信息进行恢复时,可以缓解大量的差文件叠加而占用的时间开销,提高查询效率。

五、时空检索

时空数据的检索包含两个方面的条件:时间条件和空间条件。本文主要关注时态问题(时间条件)。

基于基态修正的时空数据检索主要有两种方式:一种是基于时间点的检索,另一种是基于时间段的检索(即查询两个事件时间之间的数据)[13]。时间点检索方式的实现较为简单,当用户输入检索的时间(tj)时,首先判断与所要查找时间点之间差文件数最少的基态(基态n),然后在该基态的基础上叠加差文件,就可以得到用户所要的结果,如图3所示。

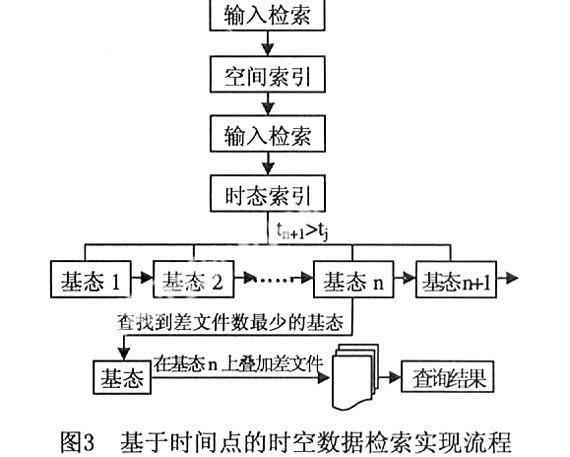
时间段的检索方式要复杂一些,根据两个事件时间所处的区域不同,分为如下的4种情况,如图4所示。

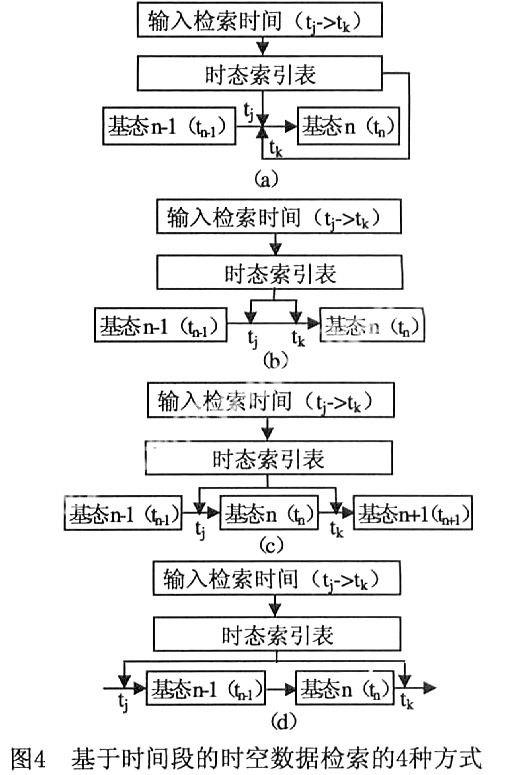
图4(a)中tj=tk,这种情况实际上就是基于时间点的检索。

图4(b)中tj与tk处于相邻的两个基态之间,两个事件时间之间没有基态的存在。这时首先计算tj时刻和tk时刻与基态n-1和基态n之间差文件数最少的基态,若tj->tn-1的差文件数小于tk->tn的差文件数,则加载基态n-1,然后在此基础上加上tn-1->tj的差文件,就得到tj时刻的快照,tj->tk时间段产生的对象就可以从tj时刻的快照到tk时刻的差文件获得;若tj->tn-1的差文件数大于tk->tn的差文件数,则加载基态n,然后在此基础上加上tn->tk的差文件,就得到tk时刻的快照,tj->tk时间段产生的对象就可以从tk时刻的快照到tj时刻的差文件获得。

图4(c)中tj与tk之间有一个基态n的存在。这时可以首先计算出tj->tn的差文件,然后再加上tn->tk的差文件,两个差文件的和就是tj与tk之间产生的对象。

图4(d)中tj与tk之间有多于1个基态的存在。首先计算出tj->tn-1的差文件,然后再计算出tn->tk的差文件。tn-1->tn的差文件只需要计算出基态n-1与基态n之间的变化情况,于是就可以得到tj->tk的差文件。

根据上面的分析,可以得到两个事件时间tj与tk之间的时空对象的查询方法,其流程如图5所示。

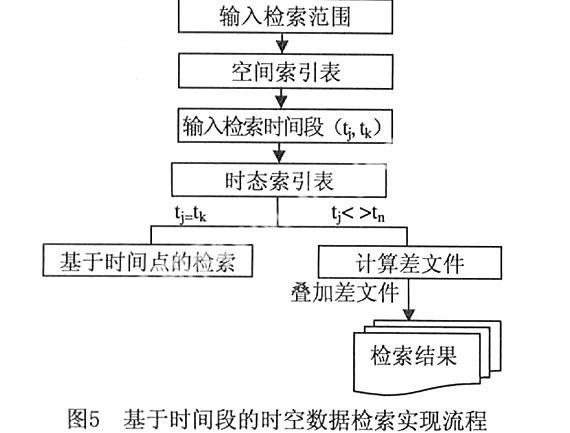
六、结论

运用动态变粒度基态距因子确定基态距阀值的方法,考虑了基态距与数据变化数量和时间查询频繁程度相关的问题,系数a的引入实现了基态动态更新,更好地优化了历史数据的存储和检索效率问题,并具备较强的实用性和灵活性。同时,针对时空数据查询分析,实现了基于时间点和时间段的不同方式的数据检索,提高了历史数据的检索效率。

基于动态变粒度的改进基态修正模型解决了数据的存储和检索问题,但对时空数据的空间关系问题并没有解决。因此,需要对基态修正模型进行进一步的扩展研究,解决对时空对象空间关系处理和时空数据的组织问题。

参考文献:

[1]刘睿、周晓光,一种基于动态基态方法的时空数据模型扩展[J].测绘通报,2008,6:50～53.

[2]Peuquet D J,Duan N.An Event-Based Spatio-Temporal Data Model(ESTDM) for Temporal Analysis of Geographical Data[J].International Journal of Geographical Information System,1995,9(1):7～24.

[3]PEUQUET D J DUAN N.An Event-based Spatio-temporal Data Model(ESTDM) forTemporal Analysis of Geographical Data[J].Intemational Journal of Geographical lnformation Systen,1995,9(1):7-24.

[4]LANGRAN G,CHRISMAN R.A Framework forTemporal Geographic lnformation[J].Cartographica1988.25(3):11-14.

[5]张祖勋、黄明智,时态GIS数据结构的探讨[J].测绘通报,1996(1):19-22.

[6]张祖勋、黄明智,TGIS数据结构的研讨[J].测绘通报,1996,(1):19～22.

[7]曹志月、刘岳,一种面向对象的时空数据模型[J].测绘学报,2002,31(1):87～92.

[8]刘仁义、刘南,基态修正时空数据模型的扩展及在土地产权产籍系统中的实现[J].测绘学报,2001,30(2):168～172.

[9]张保钢,时空数据模型在城市测绘数据库中的应用[博士学位论文].北京:中国地质大学,2005.

[10]李勇,基于GIS-T的城市公共交通时空数据模型研究及其应用[博士学位论文].广州:中国科学院,2005.

[11]余志文、张利田、邻永宏,基态修正时空数据模型的进一步扩展[J].中山大学学报(自然科学版),2004,42(1):100～103.

[12]Langran G.Temporal GIS design trade-offs//Proceedings of GIS/LIS'88[C].San Antonio:ACSM,1988:890～899.

[13]李勇、陈少沛、谭建军,基于基态距优化的改进基态修正时空数据模型研究[J].测绘科学,2007,32(1):26～29.