接触摩擦问题的扩展有限元数值模拟方法
2009-09-05董玉文任青文苏琴重庆交通大学省部共建水利水运工程教育部重点实验室重庆400074河海大学土木工程学院南京0098
董玉文,任青文,苏琴(.重庆交通大学省部共建水利水运工程教育部重点实验室,重庆400074;.河海大学土木工程学院,南京0098)
接触摩擦问题的扩展有限元数值模拟方法
董玉文1,任青文2,苏琴1
(1.重庆交通大学省部共建水利水运工程教育部重点实验室,重庆400074;2.河海大学土木工程学院,南京210098)
研究了采用扩展有限元法分析接触摩擦问题的方法。该方法基于单位分解思想,在位移插值形式中引入不连续函数和裂尖渐近位移场函数分别反映接触面的不连续性和接触面端点的奇异性;根据虚功原理建立有限元支配方程,接触面不连续函数积分采用分区高斯积分的方法。扩展有限元法在分析接触问题时不需要引入接触面单元,接触面可以位于单元内任意位置。因此该方法在分析接触摩擦问题以及压剪裂纹的开裂扩展时有显著的优势。
扩展有限元;接触摩擦;数值模拟
接触问题广泛存在于机械、土木、水利等工程领域。如混凝土坝纵缝和横缝面的接触,坝体与坝基的接触,面板堆石坝中钢筋混凝土面板与垫层之间的接触,岩体节理面或裂缝面的工作状态等。接触非线性的特点和难点在于接触边界和接触力均事先未知,而初始间隙和摩擦效应使问题变得更加困难起来。所以,摩擦接触行为的分析被认为是固体力学领域中最具有挑战性的问题之一。目前求解接触问题的方法以有限元法为主,主要算法有拉氏乘子法[1]、罚函数法[2,3]、间隙元法[4,5]、数学规划法[6]等。这些方法都需要引入层状单元、节理单元等界面单元来模拟断层、节理、裂隙等不连续面的局部接触特性,并且在模拟界面接触演化问题时,随着界面的演化,需要不断更新界面单元,重新划分网格,工作相当烦琐。
扩展有限元法(XFEM)是新兴的分析不连续问题的数值方法,在断裂力学中得到了迅速发展。由于XFEM不要求界面与单元边界一致,因而可以用来分析接触问题。与常规有限元法相比,用XFEM分析接触问题,有两个优点:①不需要在接触面上布设界面单元;②避免了随着界面的发展演化重新划分网格的麻烦。目前,用XFEM分析接触摩擦问题的研究并不多,只有John Dolbow[7]和A.R. Khoei[8]等分别采用不同的迭代算法研究接触摩擦问题。本文研究用XFEM结合增广Lagrange乘子算法分析接触问题的方法,为进一步采用XFEM分析压剪断裂问题奠定了基础。
1 接触问题的虚功方程与离散
设有2个接触体Ⅰ和Ⅱ,其可能的接触边界为Γ,两接触体在该界面上的点对可能存在的初始间隙量设为g0n(法向的相对距离),界面摩擦系数设为μ。该接触问题的虚功方程为

其中:u为位移;δu为虚位移;b为体力;¯t为面力; n为接触面上的法向矢量;tN,tT分别为接触面的法向与切向接触力。
方程(1)的形式在具体的离散过程中可以简化为更简单的形式。假定2个接触体中,Ⅰ为从接触体(slave body),Ⅱ为主接触体(master body),则方程(1)可以写为

由于在式(2)中,等式右边的项在未发生接触的边界上积分为零,而在发生接触的边界上接触力大小相等,方向相反,因此有

其中,Γc表示两接触体发生接触的边界部分。
对求解问题进行有限元离散,则上式(3)右边积分可以用从接触体上所有接触节点的和来表示:

其中,nc表示发生接触的节点数目;gNi表示节点i的法向间隙函数;gTi表示节点i的切向间隙函数(点xi在时间步内的切向相对运动距离)。
2 接触问题的XFEM模拟
2.1 扩展有限元法位移模式的构造
常规有限元法所表示的位移近似解为
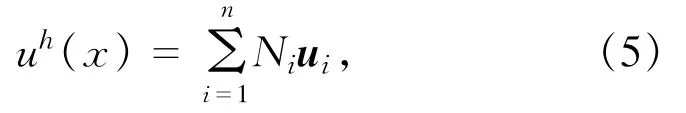
其中:Ni为节点i的插值形函数;ui为节点i的自由度向量。对于域内任意一点(x,y),插值形函数应该满足单位分解:(x,y)≡1。
Duarte和Oden[9]发现基于插值形函数的单位分解性质,可在常规有限元表达式中增加能够描述局部不连续特性的附加函数,间接反映不连续面的存在。基于单位分解思想,Belytschko等[10,11]提出了适合于描述含不连续面的近似位移插值函数,对于弹性问题,典型的表达式为

其中:N为网格中所有离散节点的集合;NΓ是被不连续面穿过、但不包含其端点的单元节点集合(图1中小方框表示的节点);N∧表示含不连续面端点的单元节点集合(图1中小圆圈表示的节点);H(x)为Heaviside函数[11],是反映不连续面位移不连续的附加函数;ai为相应的附加自由度,在不连续面上、下侧H(x)分别取+1和-1,以反映位移不连续情况,即
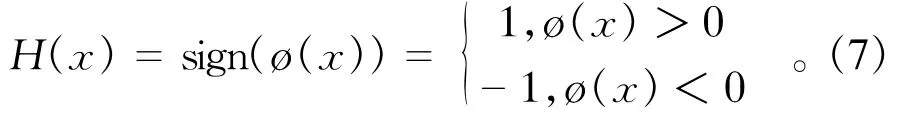
其中,式(7)中ø(x)表示不连续面的直线方程。
Φα为不连续面端点(裂尖)渐进位移场附加函数,反映端点附近的应力奇异性,bαi为相应的裂尖附加自由度;Φα通过线弹性断裂力学中裂尖渐进位移场提取得到。建立以裂尖为坐标原点的(r,θ)极坐标系(图2),则Φα由下列4个基函数组成:


图1 XFEM附加函数节点选取Fig.1 Nodes selection with XFEM additional function

图2 裂尖局部坐标系Fig.2 Local coordinate system at the crack tip
2.2 有限元支配方程的形成
对离散位移表达式(6)求导数,可以得到应变为


将式(9)和式(6)代入式(1),则可以得到以下有限元支配方程:

式中,d为域内单元节点位移列向量集合,包括节点常规自由度和附加自由度,对于常规单元,= {};对于被不连续面贯穿的单元节点i,={,};对于含端点的单元节点j,=,。f为域内单元节点力列向量集合,由单元节点力组装而成,f的形式为KC为式(1)中等式左边第一项积分后得到的整体刚度矩阵,由单元刚度矩组装而成,的形式为


式(15)中矩阵元素的上标表示对应的附加自由度。式(15)和式(14)中出现的子矩阵和外力矢量分别计算如下:

KI为式(1)中右边的含不连续面Γ项积分后得到的附加刚度矩阵,是由含接触面的不连续单元的组装而成。得到各单元的和以后,按单元节点编号对号入座,进行叠加就可以得到含接触面纹单元的单元刚度矩阵Ke,然后组装单元刚度矩阵就可以得到整体刚度矩阵,

2.3 接触面的积分方法
要计算接触面上的积分,必须对接触面进行离散。由于接触面与有限元网格是相互独立的,所以将接触面分解成许多一维单元,具体的分解方法如图所示,每个一维单元由不连续面与单元的两个交点构成(如图3)。为了对式(1)或(4)进行数值积分,在每个一维单元的两侧布置2个Gauss积分点(如图4所示),组成一对接触点对,接触面两侧任意Gauss点的δu,tN,tT通过离散插值得到。
对于某一接触点对,由式(6)可以得到两接触点之间的相对位移为

图3 不连续面数值积分时一维子单元生成方法Fig.3 Generation of 1-D subelement on the discontinuous interface for integral

图4 不连续面两侧Gauss积分点布置法Fig.4 Gauss quadrature points on each side of the discontinuous interface

其中Gauss点的位移采用母单元(四边形单元)节点位移插值得到,一维单元上Gauss点在母单元中的局部坐标的计算方法为:由一维单元上gauss点的局部坐标ξ1D计算出其整体坐标x,然后由整体坐标x反推出该gauss点在四边形母单元中的局部坐标(ξ,η),由式(21)就可以得到接触点对的相对位移。
2.4 计算接触力的Lagrange乘子法
将式(21)代入式(4),有

式(22)中的接触力tN,tT属于未知量,需要采用增量迭代法计算。本文采用用增广Lagrange乘子算法[12],即将tN,tT用Lagrange乘子代替并进行迭代。在每一级加载中,都进行Lagrange乘子迭代计算,得到真实的接触状态与接触力,并作为下一级加载的初始接触状态。
3 算例分析
图5所示为一相互接触的弹性体,尺寸为长L=1.0 m,宽b=1.0 m,弹性模量为E=2×1011Pa,泊松比μ=0.3,摩擦系数为0.3。弹性体下部固定,上部边界施加法向分布压力σ=100 kPa,切向施加分布剪力τ。XFEM模型如图6所示,采用四节点等参元,共划分单元20×25=500个,节点546个,其中接触面贯穿单元内部。为了分析界面发生滑移的过程,先施加法向压力σ,再分级施加切向剪力τ,直到两弹性体发生完全滑移结束加载。

图5 接触体模型Fig.5 Model of a contact body

图6接触体扩展有限元网格Fig.6 XFEM mesh of contact bodies
图7 是τ=25.2 kPa时的σx,σy应力分布云图,可以看出接触面上的切向方向的正应力不连续,而法向正应力连续,符合接触分析的接触面压应力条件;左下端受拉,右下端受压,与实际受力情况吻合。
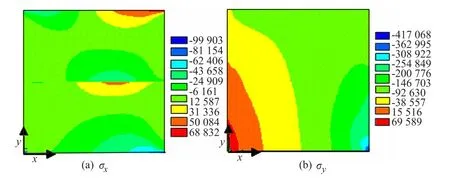
图7正应力分布图(Pa)(τ=25.2 kPa)Fig.7 Normal and tangential stress contours
图8 是不同分布剪力载荷下的剪应力分布图,从图中可以得出以下结论:①弹性体左下部剪应力在剪力载荷较小时均为负,为压剪状态,右下部均为正,为压剪状态,与实际情况吻合;②在剪力荷载较小时,接触面处于粘结状态,接触面上最大剪应力位于接触面中部,随着剪力荷载的增大,接触面逐渐发生滑移,首先发生滑移的部位在接触面剪应力较大的部位,即中部,发生滑移以后,接触面上最大剪应力的位置向后移动。
图9给出了不同剪力载荷下的接触面摩擦力分布与接触状态。可以看出剪力较小时接触面处于完全粘结状态,最大摩擦力位于接触面中部;当τ逐渐增大时,接触面会发生滑移,随着剪力荷载的增大,发生滑移的部位逐渐向后推移,最大摩擦力也逐渐向后推移;最终两接触体发生完全滑移。

图8 不同分布剪力荷载作用下的剪应力分布云图(Pa)Fig.8 The shear stress contours corresponding to different shear loadings

图9 不同分布剪力荷载作用下的接触面摩擦力分布于接触状态(Pa)Fig.9 The contact frictional stresses and contact statuses on the interface corresponding to different shear loadings
4 结语
本文将扩展有限元法与增广Lagrange乘子法结合,研究了用扩展有限元法分析摩擦接触问题的方法,通过典型算例分析,验证了方法程序的正确性。该方法与常规有限元法的不同之处是,不需要采用接触面单元,通过引入附加函数和附加自由度,使得不连续面可以位于单元内任意位置,避免了常规有限元分析接触问题时对网格划分的限制。通过Lagrange乘子的迭代,使得乘子逐渐接近于真实的接触力和真实的接触状态,达到接触分析的目的。
水利工程中岩体、混凝土的破坏形式很多属于压剪性开裂破坏,如岩质边坡、拱坝坝肩、重力坝坝踵、坝基深层滑动、板块内部地震和水库诱发地震等。由于压剪性裂纹扩展涉及到接触非线性和断裂力学结合的问题,非常复杂,实际上压剪性裂纹的开裂扩展可以分为接触摩擦和开裂扩展两个阶段,一旦裂纹面的摩擦力过大直至超过材料的抗剪强度,即进入开裂扩展阶段,本文方法为进一步采用扩展有限元法分析压剪性裂纹的开裂扩展奠定了基础。
[1]王水林,邓建辉,葛修润.改进的拉氏乘子法在接触摩擦问题中的应用[J].岩土工程学报,1998,20(5):64 -67.
[2]KIKUHCI N.A Smoothing Technique for Reduced Integration Penalty Methods in Contact Problems[J].International Journal for Numerical Methods in Engineering, 1982,(18):343-350.
[3]PERIC D,OWEN DRJ.Computational Model for 3D Contact Problems with Friction Based on the Penalty Method[J].International Journal for Numerical Methods in Engineering,1992,(35):1289-1309.
[4]雷晓燕,SWOBODE G,杜庆华.接触摩擦单元的理论及其应用[J].岩土工程学报,1994,16(3):23-32.
[5]邵伟,金锋,王光伦.用于接触面模拟的非线性薄层单元[J].清华大学学报,1999,39(2):34-38.
[6]HAUG D,SAXCE G.Frictionless Contact of Elastic Bodies by Finite Element Method and Mathematical Programming Technique[J].Computers Structures,1980, (11):55-67.
[7]DOLBOWJ,MO¨ESN,BELYTSCHKO T.An Extended Finite Element Method for Crack Growth with Frictional Contact[J].Computer Methods in Applied Mechanics and Engineering,2001,(190):6825-6846.
[8]KHOEI A R,NIKBAKHT M.An Enriched Finite Element Algorithm for Numerical Computation of Contact Friction Problems[J].International Journal of Mechanical Sciences,2007,(49):183-199.
[9]DUARTE C A,ODEN J T.An H-P Adaptive Method Using Clouds[J].Computer Methods in Applied Mechanics and Engineering,1996,(139):237-262.
[10]BELYTSCHKO T,BLACK T.Elastic Crack Growth in Finite Elements with Minimal Remeshing[J].International Journal for Numerical Method in Engineering, 1999,(45):601-620.
[11]MO¨ES N.DOLBOW J,BELYTSCHKO T.A Finite Element Method For Crack Growth Without Remeshing [J].International Journal for Numerical Method in Engineering,1999,(46):131-150.
[12]SIMOJC,LAURSEN T A.An Augmented Lagrangian Treatment of Contact Problems Involving Friction[J]. Computers and Structures,1992,42(1):97-116.
(编辑:赵卫兵)
Extended Finite Element Method of Frictional Contact Problem
DONG Yu-wen1,REN Qing-wen2,SU Qin1
(1.Key Laboratory of Hydro-Science and Engineering,Chongqing Jiaotong University,Chongqing 400074, China;2.College of Civil Engineering,Hohai University,Nanjing 210098,China)
A new method for modeling frictional contact problem by extended finite element method(XFEM)is researched.On the basis of the idea of partition of unity,a discontinuous function and the two-dimensional asymptotic crack-tip displacement fields are added to the displacement interpolation formula to account for discontinuity of the contact surface and stress singularity near the contact surface tip respectively.Governing equations are deduced by virtual work principle and the integral of the discontinuous functions are calculated by Gauss integral through sub-elements cut by discontinuous surface.Thus it is unnecessary for using contact element in contact analysis by XFEM compared with FEM,and the element can be meshed without considering the location of the contact surface.So XFEM is promising in modeling frictional contact problem and the crack growth of compression-shear mixed mode crack.
extended finite element method;frictional contact;numerical model
TV642.3
A
1001-5485(2009)05-0045-05
2008-10-17;
2008-12-17
国家重点基础研究发展计划(973项目)基金资助项目(2007CB714104);重庆交通大学省部共建水利水运工程教育部重点实验室开放基金资助项目(SLK2008B07);重庆交通大学校内青年科学基金资助项目(2008(G-08))
董玉文(1974-),男,甘肃武威人,博士、讲师,主要从事水工结构的教学与研究,(电话)13647615309(电子信箱)dongyuwen7402 @yahoo.com.cn。
