基于ＤＰＷＭ的高速高精度积分型模／数转换器

鲍志云　张　斌

摘 要:提出一种由单电源供电,基于数字脉宽调制(DPWM)原理实现、高速、高精度、积分型模/数转换器的方法。通过对按预置规律变化的脉宽调制信号实施低通滤波后与被测信号比较的方法,实现模/数转换,避免了高精度模/数转换器模拟电路设计的复杂性,并可达到较高的精度。该方法采用快速搜索算法后可进一步提高转换速度,且可方便地由单片机、DSP,FPGA等实现,还可为芯片集成提供有益的方法。

关键词:数字脉宽调制;积分型模/数转换器;可编程门阵列;脉宽调制信号

中图分类号:TH867+.91;TP368.1 文献标识码:B 文章编号:1004-373X(2009)10-153-03

High Speed and High Precision Integral A/D Convertor Based on DPWM

BAO Zhiyun1,ZHANG Bin2

(1.Shenzhen Polytechic College,Shenzhen,518055,China;2.Shenzhen Graduate School,Harbin Institute of Technology,Shenzhen,518055,China)

Abstract:A novel method based on single power supply and DPWM for A/D convertor is proposed.PWM signal which duty regulate according to the planning rules is filtered by Low Pass Filter(LPF) and LPF output compares with the measured signal.The duty is one-to-one correspondence with the A/D value when the comparator inverts.The complicated analogue circuit for high precision A/D convertion is avoided using the design method.It is a high precision integral convertor and the convertion rate can be improved by fast searching arithmetic.This method is easily realized by MCU,DSP and FPGA.It is valuably for integral chip manufacture.

Keywords:DPWM;integral A/D convertor;FPGA;PWM

0 引 言

采用数字信号处理可方便地实现各种先进的自适应算法,完成模拟电路无法实现的功能,因此越来越多的模拟信号处理正在被数字化。目前,应用较多的模/数转换器主要有积分型、逐次逼近型和Σ-Δ型模/数转换器。积分型A/D转换器一般采用双斜积分方式,其原理是将输入电压转换成时间(脉冲宽度信号)或频率(脉冲频率),然后由定时器/计数器获得数字值。优点是用简单电路就能获得高分辨率;缺点是由于转换精度依赖于积分时间,转换速率较低。Σ-Δ型A/D转换器由积分器、比较器、1位D/A转换器和数字滤波器等组成[1,2],其原理上近似于积分型,将输入电压转换成时间(脉冲宽度)信号,经数字滤波器处理后得到数字值。电路的数字部分基本上容易芯片化,因此容易做到高分辨率,但成本较高,整体芯片化较难。现有A/D转换器的原理对相关模拟器件的性能及参数要求较高,不便于集成。在需要A/D转换的应用中一般很难将高性能的A/D进行集成,需要购买相应的IP核;双斜积分型A/D等的原理因为需要负参考电压进行反向积分,一般需要双电源供电或负电压基准,这给很多应用带来不便,影响通用性,且速度较慢,一般不支持通讯和显示二者并存的功能。为了解决上述问题,采用DPWM技术进行模/数转换[3,4],一方面为缺乏A/D资源的MCU,FPGA等应用提供便利的解决方案,另一方面本方案对模拟器件的性能无特殊要求,便于集成,可用于芯片的制造,且成本较低,可适用于单电源工作,采用快速搜索算法后可使转换速率提高,同时具备通讯和显示二者并存的功能。

1 高速高精度积分型模/数转换器原理

这里采用的转换器,其基本的工作原理是通过DPWM模块产生脉宽信号(DPWM)。该信号通过简单的RC低通滤波器进行滤波后,通过比较器与被检测信号比较、处理再经比较器发出。最后通过逻辑运算模块对上述比较器发出的信号进行拾取、分析,得到被检测信号的相关信息,并发送给通讯模块及显示模块,具体方案如图1所示。该转换器采用DPWM原理实现,其发出信号的占空比与被测量有确定的对应关系,避免了高精度模/数转换器模拟电路设计的复杂性,采用快速搜索算法后可使转换速率提高[5-7]。

1.1 数字脉宽调制模块设计

该转换器的核心控制部分可由单片机、DSP,FPGA等实现。主要完成DPWM的发生、模拟信号的测量及A/D转换结果的显示控制。该设计原型采用Cyclone Ⅱ FPGA为控制芯片,其程序的整体结构如图2所示。

具体工作过程:通过锁相环得到高速时钟,用于产生高分辨率的DPWM信号;利用按一定规律调整占空比的DPWM信号实现外部电容电压的控制,与输入模拟量信号比较,直到比较器翻转,此时的Duty×Vref即为A/D转换结果。在系统中,输入50 MHz时钟,通过锁相环倍频到400 MHz,A/D转换精度达到165 μV,具体设计如图3所示,其信号功能如表1所示。

1.2 DPWM发生器设计

DPWM发生模块通过实时更新的占空比设定值,发出高分辨率的DPWM信号。在该系统中,DPWM信号的频率为20 kHz, DPWM精度为20 000个时钟周期/占空比。如图4所示,其信号功能如表2所示。

1.3 模拟量监测器设计

该模块的主要功能是实时监测对比结果INT,不断调整DUTY,得到最终的转换结果Duty display。模拟开关控制信号ASW则完成一个监测过程的控制。过程如下:电容放电→对地测量校准→模拟测量(占空比改变)→比较器翻转完成转换。以上3步不断循环[8,9]。模拟测量模块如图5所示,其信号功能如表3所示。

1.4 显示控制器模块设计

该模块主要完成通知主模块显示更新的任务,在该设计中,更新周期为100 ms。显示控制模块如图6所示,其信号功能如表4所示。

2 高速高精度积分型模/数转换器优点

2.1 满足单电源供电条件

在许多应用中出于成本或系统可靠性等考虑,采用单电源供电。传统积分型模/数转换器需采用正负双电源供电,积分器对输入电压在固定的时间间隔内积分,该时间间隔通常对应于内部计数单元的最大数,时间到达后将计数器复位,并将积分器输入连接负电源电压。在这个反极性信号作用下,积分器被“反向积分”直到输出回到零,并使计数器终止,积分器复位。积分型模/数转换器的精度可做得很高,但它们的采样速度和带宽都非常低。

在此提出的基于DPWM原理实现的积分型模/数转换器可实现单电源+5 V供电。在被测信号与DPWM信号的极性相同时,使用单电源供电的可行性显示,若被测信号与DPWM信号的极性相反时,可采用运放反相放大器的方法在单电源条件下进行极性转换,故该方案可工作在单电源条件下而无需额外增加负电源,原理如图7所示。此时,Vo=-R2Vin/R1,由于Vin<0,则Vo>0,满足单电源供电条件。

2.2 便于芯片集成

该积分型模/数转换器是采用DPWM原理实现的,模拟器件极少。它主要实现方法在于仅需要产生DPWM模块,外部仅需增加一个普通的模拟运算放大器和通信与运算等必要的逻辑单元即可;且易于在FPGA中实现,其代码可方便用于集成芯片设计。相比较而言,它比传统的模/数转换器制造高精度、高线性度的模拟单元要容易得多。该转换器设计合理,结构简单,其发出信号占空比与被测量有确定的对应关系,避免了高精度模/数转换器模拟电路设计的复杂性,便于集成芯片设计,可用于芯片的制造,且成本较低,也便于单片机和可编程门阵列等的实现。

2.3 快速搜索算法提高A/D转换速度

初始搜索采用有限步二分法、黄金分割法或随机搜索(如蒙特卡罗等方法),快速确定搜索范围,再进行占空比遍历,可大大提高A/D转换速度[10]。

2.4 采用抖动方法提高DPWM精度

由于不采用额外措施,DPWM的精度取决于开关频率和FPGA主频。为追求更高精度,可提高主频或降低开关频率。一味提高主频不现实,显著降低开关频率会影响转换速度。采用抖动方法可较方便地提高DPWM精度[2]。采用该方法可降低主频和功耗,从而降低成本。另外,还可在同等成本下提高性能。

2.5 需要注意的几个问题

比较器在临界状态会发生振荡,可考虑滞环比较和逻辑封锁的方法处理。PWM的基准需要较稳定的基准源;精度和转换速度之间的矛盾可根据具体需要加以协调;数字开关噪声的影响需要精心的布线和滤波加以抑制;可适当采用自动增益技术提高低压测量精度。

3 实验结果

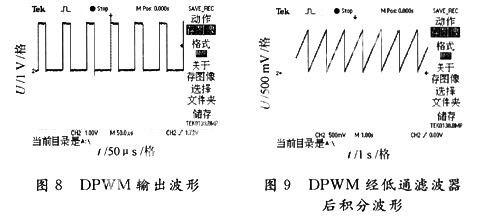
本文DPWM输出波形如图8所示。经低通滤波器后其积分测试波形如图9所示。该模/数转换器具有很高的积分线性度,分辨率为165 μV。

4 结 语

由单电源供电,基于DPWM原理实现的高速、高精度、积分型模/数转换器可方便地由单片机、DSP,FPGA等实现。无需外接模/数转换器,且便于集成芯片设计,避免了高精度A/D转换器模拟电路设计的复杂性,可为集成和相关IC设计提供有益的方法,采用快速搜索算法后可使转换速率提高,且同时具备通信和显示二者并存的功能,适用于更广泛的应用场合。

参考文献

[1]Richard Schreier,Gabor C Temes.Understanding Delta-Sigma Convertors[M].John Wiley & Sons Inc,2002.

[2]Zdravko Lukic,Nabeel Rahman,Aleksandar Prodic.Multibit ∑-Δ PWM Digital Controller IC for DC-DC Convertors Operating at Switching Frequencies Beyond 10 MHz[J].IEEE Trans.on Power Electronics,2007,22(5):1 693-1 707.

[3]Angel V Peterchev,Seth R Sanders.Quantization Resolution and Limit Cycling in Digitally Controlled PWM Convertors [J].IEEE Trans.on Power Electronics,2003,18(1):301-308.

[4]Angel V Peterchev.Digital Control of PWM Convertors:Analysis and Application to Voltage Regulation Modules[D].2002.

[5]熊海东,黄超昔,邵宇丰.FPGA设计中的编程技巧[J].现代电子技术,2005,28(2):18-20.

[6]王金明.Vcrilog HDL 程序设计教程[M].北京:人民邮电出版社,2004.

[7]Israel Koren.Computer Arithmetic Algorithms[M].AK Peters,2002.

[8]周熙,郭健民,李文宏.高精度混合型DPWM设计和实现[J].半导体学报,2007,28(6):967-974.

[9]Lee C F,Mok P K T.A Monolithic Current-mode CMOS DC-DC Convertor with On-chip Current-sensing Technique [J].IEEE JSSC,2004,39(1):3-14.

[10]王景存,王映波.基于CORDIC算法的复数除法器FPGA实现[J].现代电子技术,2008,31(24):27-30.

[11]曹新亮,樊延虎,宋永东.一种基于双积分原理的模拟量数字化实现方法.现代电子技术,2006,29(2):51-52.

[12]钟立,余水宝.单片机应用系统中高精度A/D转换电路的设计.仪器仪表用户,2006,13(2):100-103.