改进Ｈｏｕｇｈ变换的算法实现

苏志祁　尉　宇　王　涛

摘 要:利用Hough变换对直线进行检测,通常参数空间使用的是极坐标系。这种方法存在速度缓慢,结果不够精确的问题。这主要是因为极坐标所用到的正弦函数和余弦函数具有非线性特性,使将来运算基本单元的乘法不可避免。为解决这个问题,提出一种通过改换坐标系、用加法和移位运算代替乘法的新思想,大幅加快了Hough变换的速度。从而使超大型图像中,直线的实时、精确检测成为可能。

关键词:Hough变换;极坐标;标准直线方程,改进的Hough变换

中图分类号:TP311文献标识码:A

文章编号:1004-373X(2009)10-042-03

Realization for the Improved Hough Transform

SU Zhiqi,WEI Yu,WANG Tao

(Information Science & Engineering College,Wuhan University of Science and Technology,Wuhan,430081,China)

Abstract:There are some problems occur in Hough transform which generally use polar coordinates,such as low speed or inaccurate results.It is mainly caused by Sine and Cosine functions using in polar coordinates which have non-linear character,accordingly multiply is inevitable.In order to solve this problem,replacing polar coordinates and replacing multiply by addition and shift operator to speed up the process of Hough transform.Therefore,it rises the possibility to obtain in real-time and precise applications for large image.

Keywords:Hough transform;polar coordinates;standard straight line equation;improved Hough transform

0 引 言

Hough变换具有优异的鲁棒性和极佳的抗干扰能力[1-5],利用Hough变换进行直线检测,是图像分析和计算机视觉的一个重要内容[6]。但是Hough变换的计算量往往非常大,从而阻碍了其在快速、精确检测直线方面的应用。这里提出的新方法,不仅能大幅度减少Hough变换的总计算量,而且在像素允许的情况下,直线斜率的检测精度保持最高,这对于超大型图像中直线的实时、精确检测,具有重要的实用价值[7]。

1 Hough变换检测直线的原理

选取图像空间中一条直线L的某些特征作为参数空间的一个点M,并且该直线L上的所有点,通过某种算法都能够对应这些特征,从而在图像空间和参数空间之间,建立起“线-点”的对偶性[8]。Hough变换就是根据这种对偶性,将图像空间中直线的检测问题转化为参数空间中点的检测问题,而后者的处理比前者要简单得多,进行累加统计即可。

常用的Hough变换检测直线的方法,是运用下式在图像空间和参数空间之间,建立对偶变换。

ρ=xcosα+ysinα(1)

式中:ρ为极径;α为极角,取0°~180°;x为像素点相对图像原点的行坐标;y为像素点相对图像原点的列坐标。为了检测出直角坐标系中,由非零点所构成的直线,需要根据检测分辨率的要求,将ρ离散化为Nα个参数区间,将ρ离散化为Nρ个参数区间,也就是说将极坐标系量化成许多小格,建立参数空间。其核心程序代码如下:

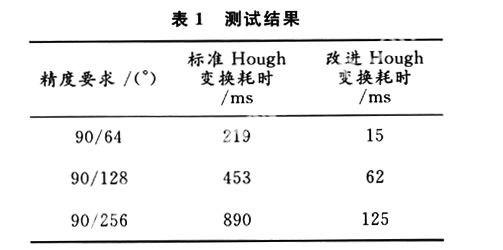
for(int i=0;i

for(int j=0;j

{

if(im.m[j][i]==feature_point)

{

for(angle=0;angle<180;angle++){

r=i*sin_tab[angle]+j*cos_tab[angle];nr=int(r+rmax);

Hough_ima.m[nr][angle]++;

}

}

}

最外层的两层循环的目的是对整个图像进行一次遍历,如果在(i,j)存在有效点,即if(im.m[j][i]==feature_point),则利用参数(i,j)在参数空间中画一条正弦曲线。这条正弦曲线的方程就是ρ=xcosθ+ysinθ。由于程序中数组的下标不能为负数,所以必须进行一次平移,也就是加上可能的负数的最大值rmax,之后就是使用一个for循环,让角度从0°~180°进行扫描,使处于正弦线上的位置全部进行累加,即Hough_ima.m[nr][angle]++。

如果需要检测出原图中的直线,还需要对Hough_ima.m进行一次遍历,搜索出最大值及它的坐标。它的值表示在原空间中一共有几个点落在这条直线上,利用它的坐标(r,θ)就可以得到ρ=xcosθ+ysinθ,进而就可以求出原直线方程y=kx+b,这样就可达到最终目的。

当然,有时还要知道这条直线的起点和终点,在获得y=kx+b之后,这个问题变得非常简单,只需要对x或者y进行一次从最小值到最大值的扫描,即可找出第一个有效点和最后一个有效点,这就是这条直线的起点和终点。

2 改进Hough变换的算法及实现

标准Hough变换其优点是:无论直线怎样变化,参数空间中α和ρ的取值范围是有限的,所以,目前的直线检测大多数都是基于这种方法。但是,这种方法在步进值较小的情况下,存在很大缺陷。步进值越小,计算量就越大。在要求检测精度很高的场合,步进值往往非常小,这样会使计算量大增。

标准Hough变换的核心原理依靠的是ρ=xcosθ+ysinθ,对比原程序r=i*sin_tab[angle]+j*cos_tab[angle]可以看到,这里用到两次查表,两次乘法以及一次加法,并且由于正弦和余弦是非线性的,所以两次乘法是不可避免的[10,11]。对于绝大多数处理,它们并不带有硬件乘法器,而必须使用软件的方法来模拟,这将耗费很多的时钟周期,使得程序运行很慢,效率很低。

在此提出并实现了一种只用加法和移位运算来实现的Hough变换,这种方法有利于在没有硬件乘法器的CPU上实现Hough变换。它使用直线方程原始定义y=kx+b。可以看到,y=kx+b所有参数都是线性的,所以不需要乘法,只需要累加就可以。但是这个方法会遇到一个问题,这里的k的范围是从正无穷到负无穷,解决的办法是只对原图进行从-45°~+45°之间的直线检测,然后将图像的(x,y)互换,再次对图像进行从-45°~+45°之间的直线检测,这样就完成了整张图片的直线检测。

for(i=0;i

for(j=0;j

if( k4_lpBits[i*k6_pitch+j*3]!=0 )

{

int s1_tmp = (i+j)<< s_Nbit;

k=(1<<(s_Nbit+1))-1;do

{

k5_mat[k][(s1_tmp>>s_Nbit)+700 ]+=1;

s1_tmp-=j;

}

while(--k);

}

上面是核心代码。变量s_Nbit是一个宏定义,决定处理的点数,从-45°~+45°有2s_Nbit个点,程序中+700的目的是为了防止数组的下标出现负数。这里使用的循环是 do-while循环,并且使用的是递减循环,而不是通常的递加循环。这个结构和汇编语言中的loop语句刚好是同一个结构,如果使用通常的for循环,将会在循环的跳转语句上浪费掉一些时间。使用递减循环的好处就是省掉一条cmp语句。下面是这段代码的反汇编。

在VS 2005中,右键单击核心语句,选择运行到光标处,再选择切换到反汇编。可以看到:

{

int s1_tmp = (i+j)<< s_Nbit;

00401977 mov ecx,edi

00401979 mov edx,7C830h

0040197E mov edi,edi

k=(1<<(s_Nbit+1))-1;do

{k5_mat[k][(s1_tmp>>s_Nbit) +700 ]+=1;

00401980 mov eax,ecx

00401982 sareax,7

00401985 add eax,edx

00401987 add dword ptr

[eax*4+404FB4h],1

0040198F lea eax,[eax*4+404FB4h]

s1_tmp-=j;

00401996 subecx,esi

} while(--k);

00401998 sub edx,7D0h

0040199E jne

}

经过优化,循环体本身几乎不消耗语句,循环变量k也被优化掉了,所以这是一段性能还算比较理想的代码。由于外层循环多一条语句少一条语句对整体性能几乎没有影响,所以本文并没有在外层循环使用do-while递减循环。

3 测试与验证

运用斜率两次查找法,能快速地检测出图像中的任意直线。这一点已经在个人计算机上经过充分的验证,并与标准Hough变换方法进行了比较。所用的软硬件环境如下:

硬件平台:CPU 为Intel,主频1 596 MHz, 内存为512 MB。

软件平台:操作系统为中文Windows XP,算法程序语言是C++,编译器用Visual C++ 2005。

以上数据是经10次测试取得平均数测试结果,它表明对于普通CPU,改进版的Hough变换确实在一定程度上提高了程序运行的效率,通过观察以上数据,改进Hough变换比标准Hough变换快8倍左右。

4 结 语

通过进一步优化程序,提高计算机配置,改进Hough变换方法,能快速、准确地检测出目标直线,这种方法使超大型图像中直线的实时、精确检测成为可能。

参考文献

[1]Lingworth J,Kittler J.A Survey of the Hough Transform[J].CVGIP,1988(44):87-116.

[2]郭强,陈桂林,童卫旗.基于变换域Hough变换的遥感图像相干干扰分析[J].光学精密工程,2001,9(2):121-126.

[3]成丹烈.利用Hough变换在序列图像中检测多个运动点目标[J].光学精密工程,1996,4(5):100-104.

[4]王绍霖,付永生.Hough变换边缘提取算法[J].同济大学学报,1996(2):471-474.

[5]袁捷,胡正仪,王延平.用Hough变换的方法提取图像拐点[J].武汉大学学报,1998(2):85-88.

[6]章毓晋.图像处理和分析[M].北京:清华大学出版社,1999.

[7]程洪玮,孙仲康.利用Hough变换实现目标检测与航迹启动[J].国防科技大学学报,1998,20(4):53-58.

[8]Foresti G,Murino V,Regazzoni C S,et al.Gruoping of Rectilinear Segments by the Labeled Hough Transform[J].CVGIP,1996,58(3):22-42.

[9]Cai Y J,Weng W.Position Control and Product DetectingBased onMachineVisionforGravure PrintingPress [J].Journal of Hunan University:Natural Sciences,2003,30(3):57-59.

[10]Yang Y Y,Deng S X.The Online Use of Image Processing Technology in Detecting Printing Registration Deviation [J].Journal of Applied Sciences,2002,20(4):423-425.

[11]Zhang R Y.Possibility and Deficiency of Automatic Pre-adjusting Inking System[J].Journal of Beijing Institute of Graphic Communication,2000,8(1):58-62.

[12]李凯南.基于Hough变换的指针式仪表的自动判读.现代电子技术,2006,29(14):18-20.

[13]粱惺彦,和卫星.改进Hough变换在PCB实时初检中应用.现代电子技术,2004,27(13):8-11.