发掘开放题的功能，提高有效性的探究

蔡有华

【摘要】开放题是指条件多余而需选择、条件不足需补充、或答案不唯一的题目。开放题因其有利于培养学生的应用意识和能力,有利于促进学生的数学交流,有利于提高学生的探究能力而越来越引起人们的关注,对数学开放题的研究,已成为当前数学改革的一个亮点。

【关键词】教学改革;开放题

Discover function of open, exaltation usefulness of investigation

Cai You-hua

【Abstract】Openning is condition surplus but need a choice, condition shortage need to be add, or answer not unique of topic.Open because it is advantageous to development a student of application consciousness and ability, be advantageous to promote student of mathematics exchanges, be advantageous to exaltation student of investigation ability but more and more cause people of concern, open to mathematics of research, have become current mathematics reform of one be a little bit bright.

【Key words】Reform in education;Open

开放题是指条件多余而需选择、条件不足需补充、或答案不唯一的题目。开放题因其有利于培养学生的应用意识和能力,有利于促进学生的数学交流,有利于提高学生的探究能力而越来越引起人们的关注,对数学开放题的研究,已成为当前数学改革的一个亮点。

1.运用条件性开放题,激发探究兴趣

条件性开放题的特点是根据所给的结论,要求从不同角度去寻找获得这个结论的条件,对不足的条件需补充,对多余的条件需取舍。解题时,促使学生作出正确的选择和判断,引发学生迫不及待地探究的兴趣,激发学生主动探究。

例1,学校乒乓球队有24人,_______________,乒乓球的人数是蓝球队的几倍?

例2,某农具厂原计划每月生产农具400件,实际9个月的产量就超过全年计划a件,这9个月实际生产农具多少件?

上述两例都要从不同角度去选择条件,如例1需填篮球队的人数,可分别为1、2、3、4、6、8、12,但要从实际出发,因篮球队至少要有5人,所以这个数字不能少于5,应选择符合实际情况的两个数字“6或8”( 12不符合,因二年级学生尚未学习除数是两位数的除法);例2中有多余条件“9个月”,还有隐含条件“全年”,解题时需选择合理而有用的条件才能得解,反之容易得出错误结论:400+a、400×9或(400+a)×9。

2.运用策略性开放题,诱发探究欲望

策略性开放题的特点是一般都给出了条件和结论,而由条件推断结论,或根据条件判断结论是否成立的策略是多样的。解题时,促使学生运用不同知识,从不同角度去探索解题的途径,有利于诱发学生探究的欲望。

例:每箱可乐都装有24罐,要使某校全年级250名学生人手一罐,至少需要多少箱?

从传统的观念看,这显然是一道除法问题,但教师没有给出相应的算式“250÷24”,而是写出这样的表达式“250?24”,这一表达刺激了学生的好奇心,促使学生用积极探究的态度和策略来思考问题。有的学生用加法,对24进行连加一直加到250,有的学生用减法,从250里连续减去24最终逼近0;有的学生试用乘法,努力发现24与什么数相乘得到250;也有学生提出用除法;还有学生提出,100包括4个25,由于250是2个100再加上半个100,如果每箱可乐都装25罐,相应的结果就是8箱再加上2箱(总共10箱),但现在每箱只有24罐,每箱少1罐,必须在第11箱中补取10罐……

由于教师具有了开放的教育理念,采取了开放式的教学方法,使一道显然被列入“封闭性”范畴的问题获得了很大的“自由度”,这说明开放题与常规题之间并没有绝对的界限,采取开放性的教学方法可促使学生运用不同知识,从不同角度去探究解题的途径,有利于培养学生思维的灵活性。

3.运用结论性开放题,体验探究乐趣

结论性开放题的特点是提供了一定的条件,满足条件的答案不是唯一的。解题时,促使学生要认真仔细地思考,才能得出不同的答案,在获取不同答案的同时,也让学生体验到了探究的乐趣。

在一节数学活动课上,教师出了这样一道题:用一张长方形的纸折一下,折出它的1/2,并画出斜线。

学生折好后,教师将不同的折法展示在黑板上(如图)

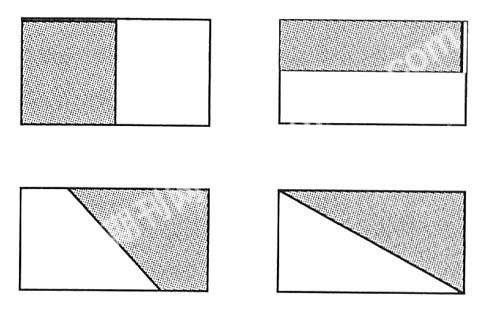
……,教师提问,还有其他情况吗?一名学生说,还有无数种折法,教师在表扬他说得好,会动脑筋的同时,又追加了一句“这无数种折法有什么共同点吗?”这时,教师让学生进行讨论,同学们兴趣盎然,纷纷发表自己的见解,最后得出“不管怎么折,都必须通过长方形的中心点。”的结论,同学们在讨论中既体验到了探究的乐趣,又让他们充分感悟、认识、理解开放题答案中的规律性、统一性,进一步提高学生的思维品质。

4.运用综合性开放题,保持探究热情

综合性开放题的特点是只给出一定的情境,其条件、解题策略和结论都要求解题者自行设计和寻找。解题时,促使学生综合地运用已有的知识去分析思考,多方构造,更好地发挥学生学习的主动性。

如教学“用24个棱长1厘米的小正方体摆成形状不同的长方体,可以摆几种?每种长方体的长、宽、高分别是多少厘米?”时,教师鼓励学生动脑筋想办法,求出问题的解。于是,有的学生采用实际操作,摆出各种不同形状的长方体;也有的学生用分解质因数的方法,得出6种形状不同的长方体,它们的长宽高厘米数分别是:①1、1、24;②1、2、12;③1、3、8;④1、4、6;⑤2、2、6;⑥2、3、4。这种设计解题方案的不唯一性,兼顾了教学的差异,赋予了探索过程勃勃生机和充沛的生命力,也使学生体验到学习本身的甘苦和力量,其学习兴趣、情感和意志都得到主动发展。

收稿日期:2009-03-27

作者地址:长汀县中区小学366300