情报信息动态规划优化网络算法软件研发与应用

〔摘 要〕动态规划是处理情报信息领域信息获取方式与路径选择，网络信息的传递与交换途径等阶段决策问题的重要方法。本研究介绍一种动态规划方法，给出了Java网络算法软件，该软件可在兼容Java的网络浏览器上运行，可用于计算最优策略和目标泛函的阶段最优和总最优值。同时，用该算法进行了用例分析，以期为有关情报信息研究与应用提供一种在线计算工具。

〔关键词〕信息;动态规划;网络算法;软件;应用

〔中图分类号〕G350.7 〔文献标识码〕B 〔文章编号〕1008-0821(2009)03-0039-03

信息获取的方式与路径选择，网络信息的传递与交换途径，以及节点与通道的搜索与选择(齐艳红，2007)，等等，都是多阶段决策问题。有关多阶段决策问题，多数可用线性规划或非线性规划来处理。然而，用动态规划处理这类问题，会更加有效(Bellman，1957)。动态规划是Bellman于20世纪50年代提出的。目前，已广泛应用于各领域的多阶段决策问题中。鉴于此，本研究建立一种Java动态规划网络算法，以期用于上述情报信息问题，可能有一定的应用价值。网络在线软件具有平台无关等优点，已在有关领域得到了应用(齐艳红，2003，2004，2006，2007)。鉴于此，本文研制了动态规划的一种网络算法软件，以期为有关情报信息研究与应用提供一种在线计算工具。

1 动态规划算法

动态规划的核心是Bellman原理:多阶段决策过程的最优决策序列有如此性质，即不论其初始阶段，初始状态，及初始决策如何，以第一个决策所形成的阶段和状态为初始条件时，随后的决策对相应的问题必须构成最优决策系列(Norton，1972;李德等，1982)。动态规划类型较多，有连续型动态规划，离散型动态规划，确定型动态规划，不确定型动态规划，等等。不同的方法，其算法也不相同。本研究所用的动态规划，为离散型确定型动态规划。算法步骤如下:

首先，将过程划分为n个阶段，k=1，2，…，n，要确定阶段k的状态x_k，x_k为阶段k的某个初始状态。

然后，要确定每阶段的决策变量。设u_k(x_k)为阶段k当状态为x_k时的决策变量，u_k(x_k)∈D_k(x_k)，其中，D_k(x_k)为阶段k的容许决策集。从阶段k到终点的决策函数序列，即子策略为:

P_kn={u_k(x_k)，u_k+1(x_k+1)，…，u_n(x_n)}

接着，要确定状态转移规则。已知阶段k的状态x_k，应用决策变量u_k，则阶段k+1的状态x_k+1可被确定，即x_k+1=T_k(x_k，u_k)。

此后，定义目标泛函。目标泛函V_kn用于评价过程的优度:

V_kn=V_kn(x_k，u_k，x_k+1，…，x_n+1)，k=1，2，…，n

其中，V_kn的最优值为最优目标泛函f_k(x_k)。目标泛函的计算公式为:

V_kn=v_k(x_k，u_k)+V_k+1n(x_k+1，…，x_n+1)

其中，v_k(x_k，u_k)为阶段k的的目标值。目标泛函是初始状态和策略的函数，故目标泛函的计算公式可写为:

V_kn(x_k，P_kn)=v_k(x_k，u_k)+V_k+1n(x_k+1，P_k+1n)

其中，P_kn={u_k(x_k)，P_k+1n (x_k+1)}。

最后，进行逆向序列最优化:

玱pt(P_kn)V_kn(x_k，P_kn)=玱pt(u_k){v_k(x_k，u_k)+玱pt(P_k+1n)V_k+1n k=n，n-1，…，1

f₁(x₁)=玱pt(P1n)V1n(x₁，P1n)

或

f_k(x_k)=玱pt(u_k∈D_k(x_k)){v_k(x_k，u_k)+f_k+1(x_k+1)} k=n，n-1，…，1

f_n+1(x_n+1)=0

此处，玱pt为最小或最大。于k=n开始，向前计算直到得出f₁(x₁)。从而，可得最优策略和目标泛函的最优值。

2 算法实现

动态规划算法dynamicprograming以Java程序设计工具包JDK研制，包括1个Java类和一个HTML文件(图1)。

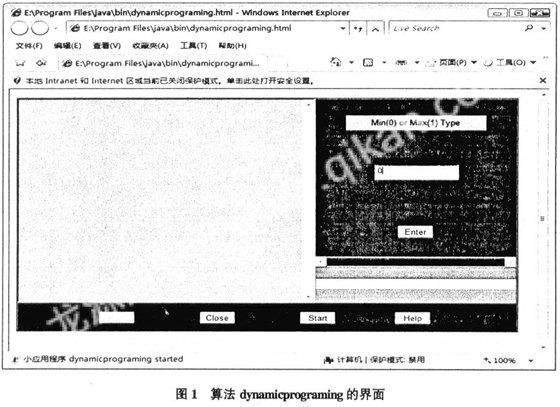
算法的Java核心代码为:

cut=0;

for(i=1;i<=m;i++)

for(k=1;k<=m;k++)

x[i][k]=10000000000;

for(i=1;i<=m;i++)

{

a[i]=10000000000;

c[i]=0;

p[i]=0;

}

for(k=1;k<=n;k++)

{

i=(int)Double.valueOf(sp.substring(0，sp.indexOf(′′))).doubleValue();

sp=sp.substring(sp.indexOf(′′)).trim();

j=(int)Double.valueOf(sp.substring(0，sp.indexOf(′′))).doubleValue();

sp=sp.substring(sp.indexOf(′′)).trim();

if(k!= n)

{

x[i][j]=Math.pow(-1D，type)*Double.valueOf(sp.substring(0，sp.indexOf(′′))).doubleValue();

}else

{

x[i][j]=Math.pow(-1D，type)*Double.valueOf(sp).doubleValue();

break;

}

sp=sp.substring(sp.indexOf(′′)).trim();

}

a[s]=0.0;

c[s]=1;

z=s;

time();

while((double)z<=1.0000000000000001E+050)

{

for(k=1;k<=m;k++)

if(!((c[k]==1)|(a[z]+x[z][k]>=a[k])))

{

a[k]=a[z]+x[z][k];

p[k]=z;

}

h=10000000000;

for(k=1;k<=m;k++)

if(!((a[k]>h)|(c[k]==1)))

{

h=a[k];

q=k;

}

if(h==10000000000)

return true;

z=q;

if(z==e)

break;

c[z]=1;

}

time();

w=a[e];

for(i=1;i>=1;i++)

{

d[i]=e;

if(e==s)

break;

e=p[e];

}

editt1.appendText(″Optimal strategy: ″);

for(;i>0;i-=2)

{

editt1.appendText(String.valueOf(d[i])+″

″+″(″+String.valueOf((int)(Math.pow(-1，type)*a[d[i]]))+″)″);

if(i==1)

break;

editt1.appendText(″---″+String.valueOf(d[i - 1])+″

″+″(″+String.valueOf((int)(Math.pow(-1，type)*a[d[i - 1]]))+″)″);

if(i==2)

break;

editt1.appendText(″---″);

}

editt1.appendText(″ ″);

if(type==1)

editt1.appendText(″Maximum benefit=″+String.valueOf((double)(int)(-w*100000)/100000)+″ ″);

else

editt1.appendText(″Minimum cost=″+String.valueOf((double)(int)(w*100000)/100000)+″ ″);

Java算法dynamicprograming的Applet被载入浏览器后，显示输入窗口。输入或选择内容依次为:最优化类型(最大化为1，最小化为0)，状态数(结点总数)，决策变量数(路径总数)，初始状态编号，终点状态编号，打开数据文件。

在数据文件中(图2)，列1为前一状态的编号，列2为后一状态的编号，列3为这两个相邻状态之间的路径的目标泛函值。数据文件为普通的MS-DOS文本文件(.txt)。在数据文件中，每个数据前后应保留至少1个空格。可在MS-DOS中的文本编辑器中编辑，或在记事本中编辑。

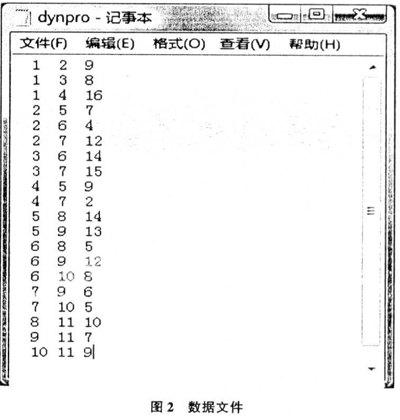
运行后输出最优策略和目标泛函的阶段最优和总最优值。

3 应用分析

一个信息获取方式与路径选择问题，要求信息获取的总耗费最小。多阶段决策过程见图3，原始数据见图2所示。这里，状态数为11，决策变量数为20。

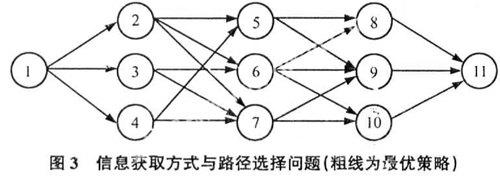
应用前述动态规划算法dynamicprograming，得到最优策略(图3)，即最优路径序列为:1→2→6→8→11;目标泛函的阶段最优值为:0→9→13→18→28;目标泛函的总最优值为28。

参考文献

[1]李德，等.运筹学[M].北京:清华大学出版社，1982.

[2]齐艳红.网络计量学的一种Internet分布式聚类分析软件[J].情报科学，2003，21(10):1069-1071，1079.

[3]齐艳红.情报信息因果分析的多变量回归模型网络软件MultiVarRegr[J].情报科学，2004，22(1):104-106，114.

[4]齐艳红.多变量情报信息的统计假设检验网络软件研究[J].情报杂志，2006，25(1):96-97.

[5]齐艳红.情报信息的判别分析网络计算软件研究[J].情报杂志，2006，25(11):64-65.

[6]齐艳红.选择网络节点与通道的Java决策树计算[J].情报科学，2007.25(Suppl.):140-141.

[7]韩玺.竞争情报人际关系网络及其构建[J].图书情报工作，2006.4:43-46，76.

[8]Bellman RE.Dynamic Programming[M].Princeston University Press.Princeston，1957:88-135.

[9]Norton M.Modern Control Engineering[M].Pergamon Press，1972:121-168.