浅谈形象思维在数学教育中的作用

陈火水

摘要形象思维是把现实世界的空间形式和数量关系联系起来的桥梁，有助于我们掌握数学知识的灵魂，真正把握数学本质，有效地获取数学知识和解决数学问题，因此，注重培养学生的形象思维能力对数学教育有很大的意义。在数学教育中，教师要不断利用体现形象思维能力的内容来锻炼学生的形象思维能力，争取使他们做到见数想形。

关键词形象思维空间形式数量关系

数学是一门研究现实世界的数量关系和空间形式的一门科学。人们经过形象思维把现实世界的空间形式和数量关系联系起来，这是数学思想的本质所在。数学思想蕴含在具体的知识中，是数学知识的“灵魂”。只有掌握了数学思想，才能真正把握数学本质，有效地获取数学知识和解决数学问题。因此，注重培养学生的形象思维能力对数学教育有很大的意义。

所谓形象思维，就是运用头脑中积累起来的表象进行的思维。其中，表象是我们以前知觉过的，然后在头脑中再现的映象。而不同类型的数学图形，正好提供了大脑形象思维的表象材料，刺激着学生的右脑思维，促使个体的左右脑得以协调发展，从而使其变得更加聪明。近年来，“仿生”这词提得越来越多，其实仿生就是指形象思维。21世纪是信息时代，即使用现代高速计算机来处理大量的数据，也已经有些力不从心了。因此，如果计算机也有形象思维，那么从形上解决很多问题就可能收到事半功倍的效果。现在很多科研工作者都在对这个方面进行研究，可见形象思维的重要性。因此，如果在初中就开始培养学生的形象思维能力，将更有利于他们未来的发展。

数与形是数学两个最基本的概念，在其发展过程中，大体上都是围绕着这两个基本概念而展开的。数体现了人的逻辑思维能力，形体现的则是人的形象思维能力，但往往形象思维比逻辑思维更直观、简单。17世纪上半叶，法国数学家笛卡尔建立了直角坐标系，从此代数和平面几何就紧密地联系起来了。在直角坐标系中，一次函数对应一条直线，二次函数对应一条抛物线。抽象的函数只要在脑中有了对应的图形，理解起来就会更加直观，许多实际问题的解决只要有了新的思路和策略，解决起来也会更加容易。但是，在我们日常的教学活动中，多是研究如何培养学生的抽象思维能力，而很少研究对形象思维的培养。在这种情况下，学生在对具体事物(图形)进行直观感知以后，当教师还没有引导他们对直观感知的材料进行概括，还没形成鲜明的形象时，就直接被动地跳到了抽象概念的学习，学生很容易对所学的知识出现一知半解的情况。因此，在平时的数学教育中，教师必须注重培养学生的形象思维能力。在初中的数学教育中。有很多内容都能体现形象思维能力：

首先，引人数轴，利用数轴让学生了解相反数、绝对值的概念，掌握有理数大小的比较方法，理解有理数加法、乘法的意义，掌握运算法则等。学生通过形象思维，能更加直观、有效地理解有理数的有关概念及运算法则。

其次，利用图像研究函数的性质，由函数解析式画出其几何图形。从而根据图形来解决问题。二次函数是学生学习的难点之一，同时又是形象思维在初中数学中体现得最为充分的部分。

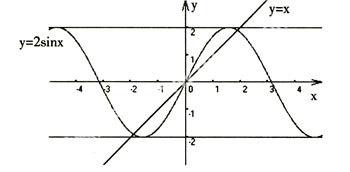
例如。求方程2Sinx=x解的个数。

解：画出函数y=2sinx，y=x的图像(如下图)：

从图形中，可以直观地看出当x>2和x<-2时，这两个函数都不可能有交点，而当一2≤x≤2时有三个交点。显然，方程Sinx=2x解的个数即是这两个函数y=sinx，y=2x的图像交点的个数，故原方程有3个不同的解。

解析：对于这道题，如果通过移项，两边同时乘、除同一数，再用平方、开方、积分、微分等常用的解方程的方法来求解，就不可能求出结果。如果根据函数的性质进行分段讨论，解题过程又会显得很复杂，且容易出错。但是利用形象思维几何的方法却能清晰、快速、且准切地求出答案，从而达到教学目标。

在解决数学问题的过程中，方法是至关重要的，如果掌握了有效的解题方法，就能够有效地节省时间、提高效率。实践也证明，运用形数结合解题会产生较好的效果，，它可以使学生进一步提高解题兴趣，激活思维，开阔思路，提高综合运用多种方法解题的能力，从而提高分析、判断、猜想、推理、决策的能力，真正提高自身的数学素质、创新精神和创新能力。因此，平时应注重培养这种思想意识，争取做到见数想形，开拓视野。

再次，在中学数学教学中，只要注意挖掘和运用数形结合进行教育活动，就能够很好地训练学生的形象思维，取得较好的教学效果。例如，通过动态的数形转换演示，帮助学生提高表象的能力；使用模型等教具和使用CAI软件演示数形转换的过程，帮助学生在头脑中建立数和形的表象：通过动态的数形转换演示，帮助学生提高联系的能力。