浅探初中数学规律题的解法

薛志阳

数学规律题,可以分为两大类,一类是应用数学规律题,一类是发现数学规律题。应用数学规律题,指的是需要学生应用以前学习过的数学规律解答的题目。发现数学规律题,指的是与学生以前学习的数学规律没有什么关系,需要学生先从已知的事物中找出规律,才能够解答的题目。学生所做数学题,绝大多数属于第一类。

由于发现数学规律题,能够增强学生的创造意识,提高学生的创新能力。因此,近几年来,人们开始逐渐重视这一类数学题。尤其是最近两年,全国多数地市的中招考试,都有这类题目。研究发现数学规律题的解题思想,不但能够提高学生的考试成绩,而且能够培养学生初步的创新精神,为学生的未来发展奠定坚实的基础。更有助于创新型人才的培养。

一、要善于抓主要矛盾

有些题目看上去很大、很复杂,实际上,关键性的内容并不多。对题目做一番认真地分析,去粗取精,取伪存真,把其中主要的、关键的内容抽出来,题目的难度就会大幅度降低,问题也就容易解决了。

例如、观察下列数表:

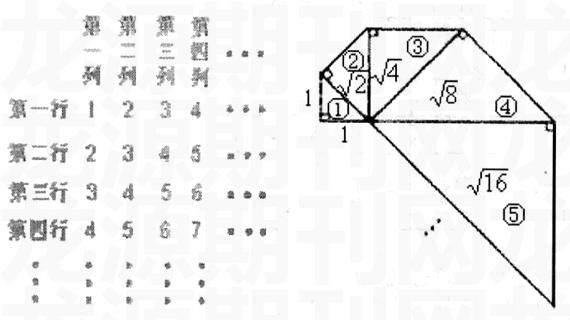
根据数列所反映的规律,第 行第 列交叉点上的数应为_____ .(乐山市2006年初中毕业会考暨高中阶段招生统一考试)

这一题,看上去内容比较多,实际很简单。题目条件里的数构成一个正方形。让我们求的是左上角至右下角对角线上第n个数是多少。我们把对角线上的数抽出来,就是

1,3,5,7,……。

这是奇数从小到大的排列。于是,问题便转化成求第n个奇数的表达式。即2n-1。

还有,邵阳市2006年初中毕业学业考试试题卷(课改区)的数学试题“图中的螺旋形由一系列等腰直角三角形组成,其序号依次为①、②、③、④、⑤……,则第n个等腰直角三角形的斜边长为_____________。”也可以按照这个思想求解。

二、 要抓题目里的变量

找数学规律的题目,都会涉及到一个或者几个变化的量。所谓找规律,多数情况下,是指变量的变化规律。所以,抓住了变量,就等于抓住了解决问题的关键。

例如,用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板,则第(3)个图形中有黑色瓷砖________块,第 个图形中需要黑色瓷砖________块(用含 的代数式表示).(海南省2006年初中毕业升考试数学科试题(课改区))

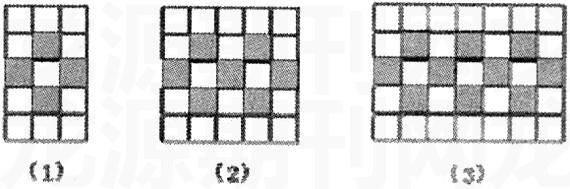
这一题的关键是求第 个图形中需要几块黑色瓷砖?

在这三个图形中,前边4块黑瓷砖不变,变化的是后面的黑瓷砖。它们的数量分别是,第一个图形中多出0×3块黑瓷砖,第二个图形中多出1×3块黑瓷砖,第三个图形中多出2×3块黑瓷砖,依次类推,第n个图形中多出(n-1)×3块黑瓷砖。所以,第n个图形中一共有4+(n-1)×3块黑瓷砖。

对于我们农村学校,学生的基础相对较差。这一题还可以利用函数来解。

序列号:1,2,3, 4, 5,……。

黑瓷砖的块数:3,7,11,15,19,……。

后面项总比前面的项大4,由此可得出块数是序列号的一次函数[可把(1,3),(2,7),(3,11),(4,15),(5,19)画在同一坐标系中,并连接各点得到一条直线。]只需选择其中的两个坐标就可求出解析式y=4n-1(y是块数,n是序列号)。

三、 要善于比较

“有比较才有鉴别”。通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。

找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。揭示的规律,常常包含着事物的序列号。所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘。

例如,观察下列各式数:0,3,8,15,24,……。试按此规律写出的第100个数是__________。”

解答这一题,可以先找一般规律,然后使用这个规律,计算出第100个数。我们把有关的量放在一起加以比较:

给出的数: 0, 3, 8, 15, 24,……。

序列号: 1, 2, 3, 4,5,……。

容易发现,已知数的每一项,都等于它的序列号的平方减1。因此,第n项是n2-1,第100项是1002-1。

四、要善于寻找事物的循环节

有些题目包含着事物的循环规律,找到了事物的循环规律,其他问题就可以迎刃而解。

譬如,玉林市2005年中考数学试题:“观察下列球的排列规律(其中●是实心球,○是空心球):

●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……

从第1个球起到第2004个球止,共有实心球 __________个。”这些球,从左到右,按照固定的顺序排列,每隔10个球循环一次,循环节是●○○●●○○○○○。每个循环节里有3个实心球。我们只要知道2004包含有多少个循环节,就容易计算出实心球的个数。因为2004÷10=200(余4)。所以,2004个球里有200个循环节,还余4个球。200个循环节里有200×3=600个实心球,剩下的4个球里有2个实心球。所以,一共有602

个实心球。有类似的题目:已知:3¹=3,3²=9,3³=27,3⁴=81,3⁵=243,3⁶=729……,求3²⁰⁰⁷的个位数字是_______。个位数每

隔4次循环一次,循环节是3,9,7,1。当指数是4的倍数时,个位数字都是1。我们只要知道2007包含有多少个循环节,就容易计算出个位数字。因为2007÷4=501(余3)。所以,2007次里有501个循环节,还余3次。所以只需循环节在往后移3个就得出答案为9。

五、要进行计算尝试

找规律,当然是找数学规律。而数学规律,多数是函数的解析式。函数的解析式里常常包含着数学运算。因此,找规律,在很大程度上是在找能够反映已知量的数学运算式子。所以,从运算入手,尝试着做一些计算,也是解答找规律题的好途径。例如1:汉川市2006年中考试卷数学“观察下列各式:0,x,

x2,2x3,3x4,5x5,8x6,……。试按此规律写出的第10个式子是__________。”

这一题,包含有两个变量,一个是各项的指数,一个是各项的系数。容易看出各项的指数等于它的序列号减1,而系数的变化规律就不那么容易发现啦。然而,如果我们把系数抽出来,尝试做一些简单的计算,就不难发现系数的变化规律。

系数排列情况:0,1,1,2,3,5,8,……。

从左至右观察系数的排列,依次求相邻两项的和,你会发现,这个和正好是后一项。也就是说原数列相邻两项的系数和等于后面一项的系数。使用这个规律,不难推出原数列第8项的系数是5+8=13,第9项的系数是8+13=21,第10项的系数是

13+21=34。所以,原数列第10项是34x9。

例如2:

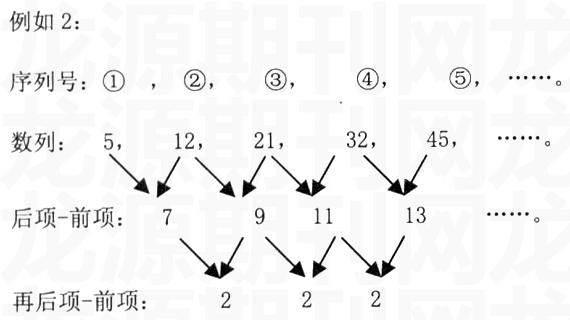
象符合这种情形的关系,数就是关于序列号的二次函数,求出它的解析式就可以了。类似的还有指数函数型的数列:2,4,8,16……函数关系为y=2n。

“条条道路通罗马”。解答找规律这一类题的思路有许多条,这里只是把“常用”的解题思路做一个简单的总结。学生应该建立数感,符号感,发展抽象思维。在解题过程中充满了观察,实验猜想,验证,推理与交流等丰富多彩的数学活动。有兴趣的老师还可以从解方程组的角度、拉格郎日插值定理的角度、求函数解析式的角度进一步研究解决这一类问题的新途径。