Calculation of Transport Properties of CF4+Noble Gas Mixtures
2009-05-15SoodabehNikmaneshJalilMoghadasiandMohammadMehdiPapari
Soodabeh Nikmanesh*, Jalil Moghadasiand Mohammad Mehdi Papari
Calculation of Transport Properties of CF4+Noble Gas Mixtures
Soodabeh Nikmanesh1,*, Jalil Moghadasi1and Mohammad Mehdi Papari2
1Department of Chemistry, Shiraz University, Shiraz 71454, Iran2Department of Chemistry, Shiraz University of Technology, Shiraz 71555-313, Iran
The present work is concerned with determining the viscosity, diffusion, thermal diffusion factor and thermal conductivity of five equimolar binary gas mixtures including: CF4-He, CF4-Ne, CF4-Ar, CF4-Kr, CF4-Xe from the principle of corresponding states of viscosity by the inversion technique. The Lennard-Jones (12-6) model potential is used as the initial model potential. The calculated interaction potential energies obtained from the inversion procedure is employed to reproduce the viscosities, diffusions, thermal diffusion factors, and thermal conductivities. The accuracies of the calculated viscosity and diffusion coefficients were 1% and 4%, respectively.
corresponding states principle, diffusion, inversion method, kinetic theory of gases, thermal conductivity, transport properties, viscosity
1 INTRODUCTION
Tetrafluoromethane which is a low temperature refrigerant is employed in electronics microfabrication alone or in combination with oxygen as a plasma etchant for silicon, silicon dioxide, and silicon nitride. This compound is a potent greenhouse gas that contributes to the greenhouse effect. It is very stable, has an atmospheric lifespan of 50000 years, and a high greenhouse warming potential of 6500 (CO2has a factor of 1); however, the low amount in the atmosphere restricts the overall radiative forcing effect. Although structurally similar to chlorofluorocarbons (CFCs), tetrafluoromethane does not deplete the ozone layer.
The results of kinetic and statistical-mechanical theories provide theoretical expressions for various equilibrium and non-equilibrium (transport) properties in terms of the potential energy of interaction between a pair of molecules [1]. Thus, the evaluation of the thermophysical properties of fluids will be straightforward if a pair potential energy is already known. This procedure reduces the need for experimentation to a manageable level. For instance, the most successful and promising approach of this type is the calculation of the transport properties of dilute gases from the known pair-wise interaction potential energy using the kinetic theories of gases initiated by Boltzmann and developed by Chapman and Enskog [2]. Therefore, the problem is now how to establish the intermolecular pair potential energy for a specific system.
Among thermophysical properties, the viscosity is almost independent of the existence of the internal degrees of freedom and unaffected by inelastic collision. This is particularly valuable because it can be served to infer the potential energy. The viscosity coefficients are obtained either from the resistance of the gas to flow a capillary tube or by observing the damping effect of the gas upon the motion of a torsionally oscillating disc [3].
The general method of inferring molecular interactions from transport properties such as viscosity was essentially cuts and trials on a model potential until a good fit was obtained to a given set of experimental data on thermophysical properties. The major problem is increasing difficulties for fixing the adjustable parameters with experiments as their number increases. In addition, this procedure does not produce a unique potential. The second approach is the inversion method that generates a spherical pair potential energy without introducing any disposable model potential.
Papari. [4-8] have developed this method to examine intermolecular potential energies and then predict transport properties of some selected gas mixtures.
The present work is devoted to the calculation of the gas transport coefficients of five CF4-noble gas mixtures using the inverted unlike pair potential energy through the Chapman-Enskog [2] and Wang Chang-Uhlenbeck [9] solutions of the kinetic theories of gases as well as Ross scheme [10].
2 MOLECULAR THEORY OF TRANSPORT PROPERTIES OF GASES




Whereis the scattering angle,(l)() is the transport collision integral,is the impact parameter,is the relative kinetic energy of colliding partners,is the relative velocity of colliding molecules,mis the closest approach of two molecules, andBis the molecular thermal energy. Hence, the potential() would serve as the input information required in calculating collision integrals and, consequently, the transport properties. The definition of collision integrals as dimensionless reduced quantities makes calculations of transport properties more convenient.
We can introduce the reduced collision integral*(l,s)as follows:

The ratios of collision integrals are given by:





3 INVERSION SCHEME
The inversion procedure developed by Smith and coworkers [11-13] and fully described in our previous work [14] is briefly given here. Also, we calculated transport properties of some polyatomic gases including carbon tetrafluorid (CF4), sulfur hexafluoride (SF6), and nitrous oxide (N2O) [15]. This method relies on the Chapman-Enskog rigorous kinetic theory of gases, which is well developed for spherical interactions. The method is iterative and converges rapidly once a good choice has been made for the initial potential starting the iteration.



In Eq. (10)*isB/andis the well depth. Eqs. (10) and (11) are central equations in the inversion scheme.
The new potential is a closer approximation to the true potential energy than the potential of the initial model. The new() can be obtained from square interpolation among new potentials. The new potentials are used to calculate improved collision integrals by performing three consecutive integral Eqs. (1)-(3). The above-mentioned process is repeated until convergence occurs. The convergence condition is the degree to which the calculated collision integrals for a given iteration are close to the experimental correlations within experimental accuracy. It should be mentioned that the rate of convergence of iteration reflects the differences of the detail between the initial potential and the potential obtained around iteration. In general, of course, the closer is two potentials functions, the faster is the convergence. The present results converged after two iterations.
4 RESULTS AND DISCUSSION
In this study an iterative inversion procedure has been employed to define the intermolecular pair interaction potential energies of CF4+noble gas gaseous mixtures from corresponding states of viscosity. To implement the full inversion procedure, the experimental data should be extended over as wide temperature range as possible. In this respect, a corresponding states correlation for viscosity collision integral was taken from Ref. [16] to calculate the reduced viscosity collision integral*(2,2).
The inverted potential energies for all systems have been used to evaluate improved collision integrals through Eqs. (1)-(3). The calculated collision integrals and their ratios for aforementioned systems are given in Tables 1-5. The relationships given by Ross. [10] and equations obtained from Chapman- Enskog solution of the Boltzman equation [2, 3, 17] have been employed to compute, respectively, thermal conductivity and other remaining transport properties of present systems by the use of improved collision integral ratios given in Tables 1-5.
Figures 1-4 demonstrate the deviations of the calculated viscosity values of afore-cited mixtures from those reported in Refs. [18] and [19] at different temperatures and mole fractions. Figs. (1)-(4) depict that the calculated viscosities agree with experimental values within 1%. Unfortunately, due to lack of experimental data, we could not confirm the obtained viscosity of CF4-Xe mixture. In addition, the comparison of the calculated viscosities with those calculated from Davidson’s and Reichenberg’s methods [20, 21] are brought in Figs. 5 and 6, respectively. In the case of three heavier noble gas mixtures, the relative errors are at most 0.9% in comparison with those estimated using Davidson’s method [20] and at most 0.5% when compared with the Reichenberg’s method [21]. But the deviations of estimated values for CF4-He and CF4-Ne mixtures from those obtained using Davidson’s and Reichenberg’s methods increase at very low and very high temperatures. The calculated interaction viscosities were correlated with the following function:

Table 1 The reduced collision integrals and their ratios for CF4-He system

Table 2 The reduced collision integrals and their ratios for CF4-Ne system

Table 3 The reduced collision integrals and their ratios for CF4-Ar system

Table 4 The reduced collision integrals and their ratios for CF4-Kr system

Table 5 The reduced collision integrals and their ratios for CF4-Xe system

Figure 1 Deviations of the calculated viscosity values of CF4-He gaseous system from those reported in Ref. [18] at different temperatures and mole fractions
(He):◆ 0.3748;■ 0.5209;▲ 0.9134


Figure 2 Deviations of the calculated viscosity values of CF4-Ne gaseous system from those reported in Ref. [18] at different temperatures and mole fractions
(Ne): ◆ 0.1713; ■ 0.3886;△ 0.5801; × 0.8041

Figure 3 Deviations of the calculated viscosity values of CF4-Ar gaseous system from those reported in Ref. [18] at different temperatures and mole fractions


Figure 4 Deviations of the calculated viscosity values of CF4-Kr gaseous system from those reported in Ref. [19] at different temperatures and mole fractions
(Kr): ◆ 0.2122;□ 0.2899;▲ 0.5127

Figure 5 The comparison of the calculated viscosities with those calculated from Davidson’s method [20]

Figure 7 shows how the calculated diffusion coefficients of aforesaid systems except CF4-Xe mixture, deviate from those given in Refs. [18, 19]. The accuracy of this property is of the order of 4%. Also the values of diffusion coefficients were correlated with the following equation:


Figure 6 The comparison of the calculated viscosities with those calculated from Reichenberg’s method [21]
◆ CF4-He;■ CF4-Ne;△ CF4-Ar; × CF4-Kr;○ CF4-Xe
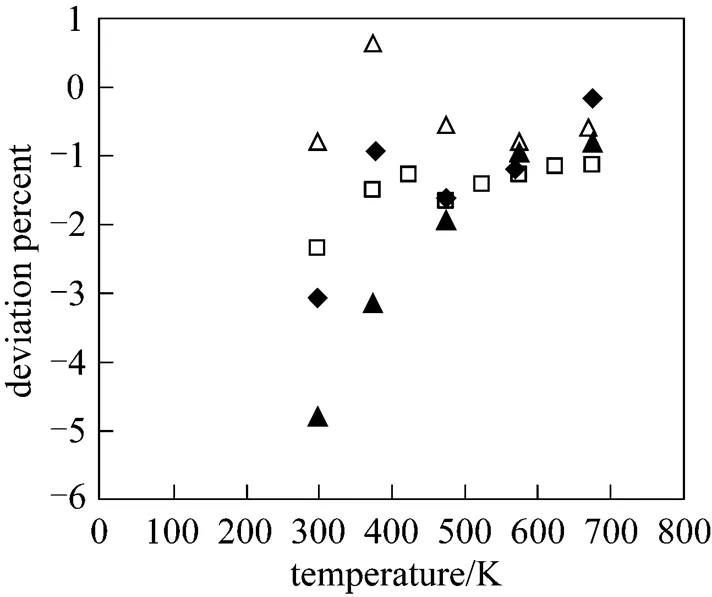
Figure 7 Deviation plot for the diffusion coefficients at different temperatures: for CF4-He, CF4-Ne, CF4-Ar compared with Ref. [18], for CF4-Kr compared with Ref. [20]
◆ CF4-He; ▲ CF4-Ne; □ CF4-Ar;△ CF4-Kr
As for thermal conductivity, the predicted viscosities obtainedthe inverted pair potential energies were employed to predict thermal conductivities using Ross.’s method [10]. The calculated interaction thermal conductivities were correlated with the following polynomial:

The parameters are listed in Table 8. Unfortunately, because of lack of the literature data of thermal diffusion factors and thermal conductivities, we could not evaluate the accuracy of our work.
5 CONCLUSIONS
The present study describes a procedure for analyzing the viscosity data in the form of corresponding states equations to yield a unique unlike effective and isotropic pair potential energy of the CF4-He, CF4-Ne, CF4-Ar, CF4-Kr and CF4-Xe systems.
The acceptable agreement was achieved between the calculated and the literature values for viscosity and diffusion coefficients. No literature data are now available to assess the accuracy of thermal conductivity and thermal diffusion factors calculated with the present method.
Using this procedure, there is no need to set flexible multi-parameter potential functions. The major benefit of our studies has been that in addition to the prediction of viscosity with an acceptable accuracy, the inverted pair potential energy is capable of providing other transport properties such as the binary diffusion coefficient, thermal diffusion factor, and thermal conductivity. Therefore, the most crucial advantage of the inversion procedure is that the values of one property that is known accurately can be used to predict other properties that are known less accurately from the experiment.

Table 6 Least squares coefficients, correlation coefficients (R), and standard errors (ES) for Eq. (12)

Table 7 Least squares coefficients, correlation coefficients and standard errors for Eq. (13)

Table 8 Least squares coefficients, correlation coefficients and standard errors for Eq. (14)
ACKNOWLEDGEMENTS
.
NOMENCLATURE
*ratio of collision integrals
a,a,a,aconstant
*ratio of collision integrals
impact factor, m
b,b,b,bconstant
*ratio of collision integrals
c,α,cconstant
binary diffusion coefficient, m2·s-1
α,d,dconstant
*ratio of collision integrals
Sstandard error
econstant
* ratio of collision integrals
inversion function
BBoltzman constant, J·K-1
molecular mass, kg
(l)transport cross-section, m2
correlation coefficient
intermolecular distance, m
mclosest approach of two molecule, m
temperature, K
*reduced temperature
() intermolecular potential energy, J
relative velocity of colliding molecules
mole fraction
energy-scaling factor, J
interaction viscosity, Pa·s
scattering angle, rad
interaction thermal conductivity
length-scaling factor, m
Ω(l,s)collision integral, m2
Ω*(l,s)reduced collision integral
Superscripts
,weighting factors related to the mechanism of transport by molecular collisions
* reduced
Subscripts
diffusion
thermal diffusion factor
viscosity
thermal conductivity
1 Hirschfelder, J.O., Curtis, C.F., Bird, B.R., Molecular Theory of Gases and Liquids, John-Wiley, New York (1964).
2 Chapman, S., Cowling, T., The Mathematical Theory of Non-Uniform Gases, 3rd edition, Cambridge University Press, Cambridge (1964).
3 Wakeham, W.A., Nagashima, A., Sengers, J.V., Measurements of the Transport Properties of Fluids, Experimental Thermodynamics, Blackwell Scientific Publications, Oxford (1991).
4 Papari, M.M., Boushehri, A., “Semi-empirical calculation of the transport properties of eight binary gas mixtures at low density by the inversion method”,..., 71, 2757-2767 (1998).
5 Haghighi, B., Fathabadi, M., Papari, M.M., “Calculation of the transport properties of CO-nobel gases mixtures at low density by the semi-empirical inversion method”,..., 203, 205-225 (2002).
6 Haghighi, B., Javanmardi, A.H., Najafi, M., Papari, M.M., “Calculation of the diffusion coefficients for mixtures of NO with He, Ne, Ar and Kr at low density using semi-empirical inversion method”,...., 2 (3), 371-384 (2003).
7 Papari, M.M., Mohammad-Aghaie, D., Haghighi, B., Boushehri, A., “Transport properties of argon-hydrogen gaseous mixture from an effective unlike interaction”,..., 232,122-135 (2005).
8 Papari, M.M., Mohammad-Aghaie, D., Moghadasi, J., Boushehri, A., “Semi-empirically based assessment for predicting dilute gas transport properties of F2and Ar-F2fluids”,..., 79, 67-74 (2006).
9 Wang Change, C.S., Uhlenbeck, G.E., de Boer, J., “The heat conductivity and viscosity of poly-atomic of gases”, de Boer, J., Uhlenbeck, G.E., Eds., Studies in Statistical Mechanics, North-Holland, Amsterdam (1964).
10 Ross, M.J., Vesovic, V., Wakeham, W.A., “Alternative expressions for the thermal conductivity of dilute gas mixtures”,, 183,519-536 (1992).
11 Gough, D.W., Maitland, G.C., Smith, E.B., “The direct determination of intermolecular potential energy functions from gas viscosity measurements”,.., 24 (1), 151-161 (1972).
12 Maitland, G.C., Smith, E.B., “The direct determination of potential energy functions from second virial coefficients”,.., 24,1185-1201 (1972).
13 Clancy, P., Gough, D.W., Mathews, G.P., Smith, E.B., Maitland, G.C., “Simplified methods for the inversion of thermophysical data”,.., 30, 1397-1407 (1975).
14 Papari, M.M., “Transport properties of carbon dioxide from an isotopic and effective pair potential energy”,.., 288, 249-259 (2003).
15 Moghadasi, J., Papari, M.M., Nekoie, A., Sengers, J.V., “Transport properties of some polyatomic gases from isotropic and effective pair potential energies (part II)”,.., 306, 229-240 (2004).
16 Bzowski, J., Kestin, J., Mason, E.A., Uribe, F.J., “Equilibrium and transport properties of gas mixtures at low density: Eleven polyatomic gases and five noble gases”,...., 19, 1179-1232 (1990).
17 Papari, M.M., Moghadasi, J., Yousefi, F., Boushehri, A., Haghighi, B., “Correlation and prediction of low density Ne-H2 gas transport coefficients”,..., 10, 143-156 (2008).
18 Kestin, J., Khalifa, H.E., Ro, S.T., Wakeham, W.A., “The viscosity and diffusion coefficients of eighteen binary gaseous systems”,, 88, 242-260 (1977).
19 Kestin, J., Khalifa, H.E., Wakeham, W.A., “The viscosity of gaseous mixtures containing Krypton”,..., 67 (9), 4254-4259 (1977).
20 Davidson, T.A., “A simple and accurate method for calculating viscosity of gaseous mixtures”, U.S. Bureau of Mines, RI9456 (1993).
21 Reichenberg, D., “New simplified methods for the estimation of the viscosities of gas mixtures at moderate pressures”, Natl. Eng. Lab. Rept. Chem. 53, East Kilbride, Glasgow, Scotland (1977).
2009-01-05,
2009-06-25.
* To whom correspondence should be addressed. E-mail: soodabeh.nikmanesh@gmail.com
杂志排行
Chinese Journal of Chemical Engineering的其它文章
- Molecular Simulation of CO2/H2 Mixture Separation in Metal-organic Frameworks: Effect of Catenation and Electrostatic Interactions*
- Deactivation Kinetics of Nitrile Hydratase in Free Resting Cells*
- Corrosion Behavior of TP316L of Superheater in Biomass Boiler with Simulated Atmosphere and Deposit
- Influence of A-type Zeolite on Methane Hydrate Formation*
- Effects of Sintering Atmosphere on the Microstructure and Surface Properties of Symmetric TiO2Membranes*
- Improvement of Isomerization Process of Crude Isoamylene with Tertiary-amyl-alcohol Addition
