Prediction of Critical Endpoints Based on the PR Equation of State*

YANG Quan (杨全)**, ZHU Shenlin (朱慎林) and LI Yigui (李以圭)



Prediction of Critical Endpoints Based on the PR Equation of State*

YANG Quan (杨全)1,**, ZHU Shenlin (朱慎林)2and LI Yigui (李以圭)2

1Key Laboratory of Energy Resources & Chemical Engineering, Ningxia University, Yinchuan 750021, China2Department of Chemical Engineering, Tsinghua University, Beijing 100084, China

In the design of chemical processes, such as catalytic cracking of bitumen and heavy oil, the knowledge of phase behavior at the critical endpoint is essential. Based on the PR equation of state, the algorithm developed by Heidemann and Khalil for calculating critical properties was used to compute critical points. An algorithm for determining the equilibrium phase of the critical point using the tangent plane criterion was developed, and was used to calculate the critical endpoints of different mixtures, including non-polar, polar and associating systems. The critical endpoint, representing the type of the phase behavior, was employed to fit the interaction parameter of mixtures in critical state at high pressure. Lines of critical endpoints for ternary mixtures were also determined with the algorithm.

critical endpoint, PR equation of state, interaction parameter

1 INTRODUCTION

The phase behavior at a critical endpoint (CEP) for mixtures is very complex. In a global phase diagram in Temperature-Pressure space for a mixture, critical endpoints are at the end of a critical line. When a vapor or liquid equilibrium phase is in equilibrium with a critical phase, the corresponding phase point is a critical endpoint. In chemical engineering, to solve many problems, such as the design for catalytic cracking of bitumen and heavy oil, the knowledge of phase behavior at the critical endpoint is needed. In phase diagrams of mixtures, the critical endpoints are important and determine the type of phase diagrams [1]. The existence of critical endpoints is related to the instability of the critical phases and the equilibrium of multiple phases.

Critical endpoints may be divided into two types. When a vapor-liquid critical phase is in equilibrium with a liquid phase, the corresponding critical endpoints belong to the first type. When a liquid-liquid critical phase is in equilibrium with a vapor phase, it is the second type. The phase in equilibrium with a critical phase is named equilibrium phase. The pressure at the critical endpoint is high and only some mixtures with certain composition have critical endpoints. To determine critical endpoints experimentally, expensive apparatus is needed and it is also difficult to obtain accurate results. A cubic equation of state, the PR equation of state, has been employed to calculate critical endpoints herein. It is widely used to compute critical properties [2] and presents better precision in predicting liquid properties compared with the RKS equation of state [3]. Many techniques were developed to compute the critical properties [4, 5]. Li [6] proposed an algorithm for predicting the critical temperature. Kreglewski and Kay [7] computed the critical pressure. Chueh and Prausnitz [8] developed an algorithm for calculation of critical temperature, pressure and volume. Based on the PR equation of state, Peng and Robinson [2] developed a technique for predicting critical properties using thermodynamic criterion, which was more applicable than the algorithm of Kreglewski and Kay and that of Chueh and Prausnitz, but involved computing very large determinants. Heidemann and Khalil [9] developed a technique taking the temperature, volume and compositions as independent variables to obtain the critical condition. This method is rather stable and converged rapidly, and is used most frequently. The method is thus employed to compute the critical points in this study, and the tangent plane criterion [10, 11] is used to calculate the equilibrium phase.

2 THE PR EQUATION OF STATE

In this study, the PR equation of state [12] is adopted, which is presented in the following form:

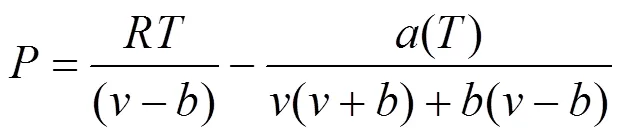
whereandare the energy parameter and the size parameter, respectively. The two parameters for the mixturesare evaluated using the van der Waals mixing rules:

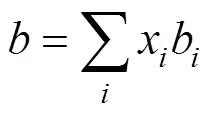
whereKis the interaction parameter for componentsand. UsuallyKK. Zhu. [3] stated that the values of the interaction parameters should be modified according to pressure and temperature for improving the precision of calculations and thus presented by different expression in different pressure range.

3 ALGORITHM

3.1 Computation of critical points

In the algorithm of Heidemann and Khalil [9], the temperature and volume were taken as independent variables. At a critical point, the following equation obtained after the Helmholtz free energy was expanded in a Taylor series must be satisfied:

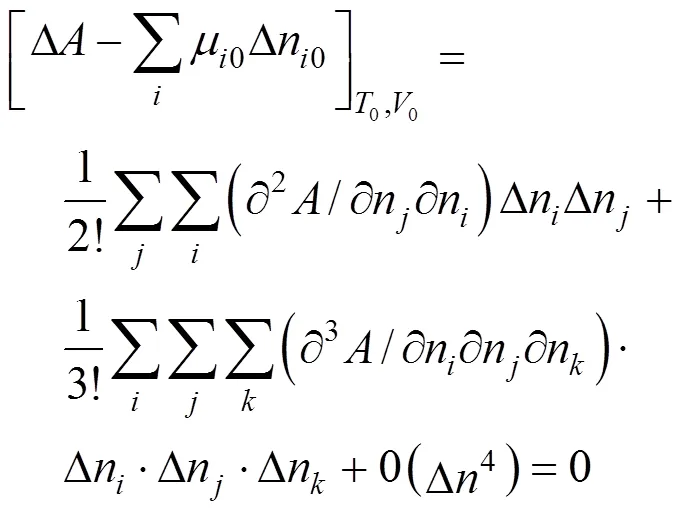
The quadratic term and the cubic term must be zero:

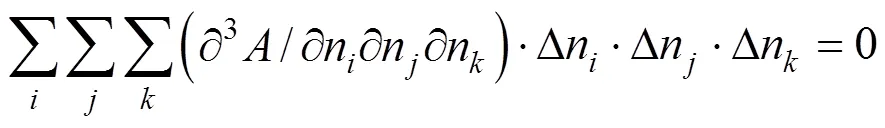
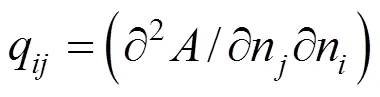
The derivatives in Eqs. (6) and (7) can be replaced as

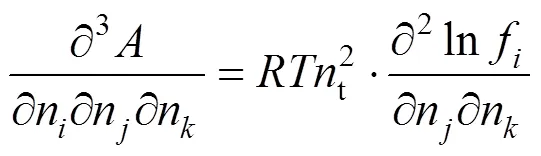
With Eqs. (6) and (7), the critical points at different composition for different mixtures can be evaluated using the Newton-Raphson method.

3.2 The tangent plane criterion

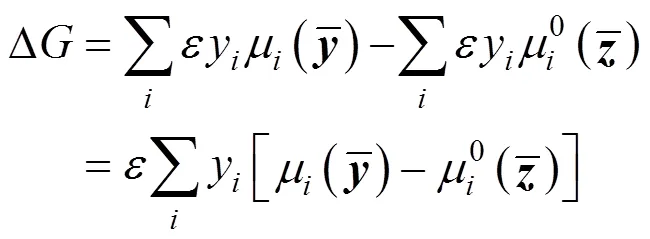
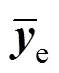
To calculate the composition of the equilibrium phase, assuming

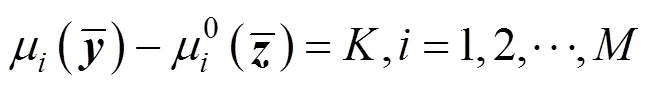
The expression of chemical potential is

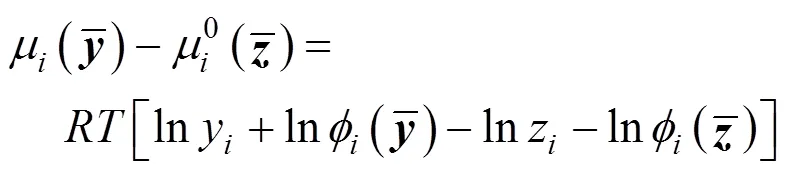
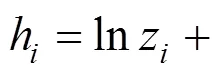
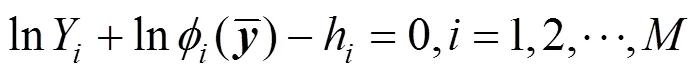
With the PR equation of state, Eq. (14) is derived to calculate the fugacity coefficient of a component in a mixture. Eqs. (2) and (3) gives the corresponding mixing rules.

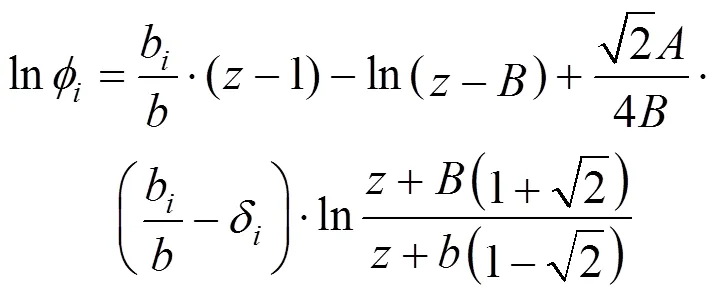
where

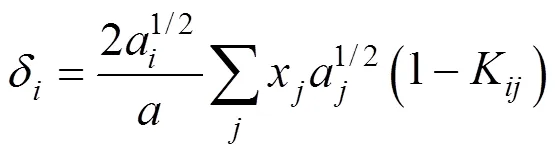
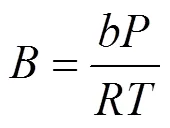
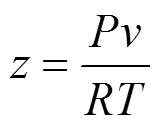
The successive substitution method [13, 14] is employed to solve Eq. (13). After obtainingYfor the previous iteration, the compositionyfor the next iteration is calculated using the following equation:

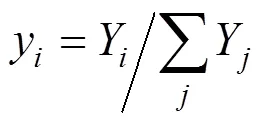
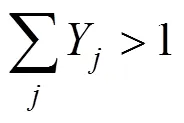
4 RESULTS AND DISCUSSION

The critical endpoints of some mixtures, including non-polar, polar and associating systems, were calculated using the algorithm. Based on the study of Zhu. [3], the critical endpoint was employed to correlate the interaction parameter of mixtures in critical state at high pressure.

The computation results for the critical endpoints of the methane (1)--hexane (2) and the ethane (1)-ethanol (2) mixtures and the corresponding interaction parameters are presented in Tables 1 and 2, where1ande,1represent the mole fraction of component 1 in the critical phase and the corresponding equilibrium phase, respectively. The calculation results show that the critical endpoints are sensitive to the value of interaction parameter. If the interaction parameter is fitted with other methods, such as the bubble point pressures, is employed to calculate the critical endpoints, the accuracy of the critical endpoints may be lower.

Table 1 Computed critical endpoints for methane (1)-n-hexane (2) mixture

Table 2 Computed critical endpoints for ethane (1)-ethanol (2) mixture

Fitted with the experimental values at critical endpoint for the methane (1)--hexane (2) and the ethane (1)-ethanol (2) mixtures in Table 3, the interaction parameter is 0.013 for methane (1)--hexane (2) and 0.133 for ethane (1)-ethanol (2). The objective function for the fitting is as follows:

The algorithm is stable and converges rather rapidly, with several iterations. It can be applied to calculate the critical endpoints of different mixtures, including non-polar, polar and associating systems. The available experimental data for the mixtures are listed in Table 3, and the calculated results are presented in Table 4. The interaction parameters in Table 4 are fitted by the experimental data in Table 3 and used to determine the critical endpoints in Table 4.

Table 3 The experimental critical endpoints for some mixtures [15-18]

The errors in the computed temperatures at critical endpoints are small, but the errors in the pressure calculation are larger. In Table 4, the largest error in the calculated pressure is 3.76%, but it is small compared with the errors in evaluating the critical pressure of associating mixtures employing the equation of state. van Konynenburg and Scott [1], and Gubblns. [19] reported a 5% error in the calculated pressure and the error was 20% in the study of Chen[20].

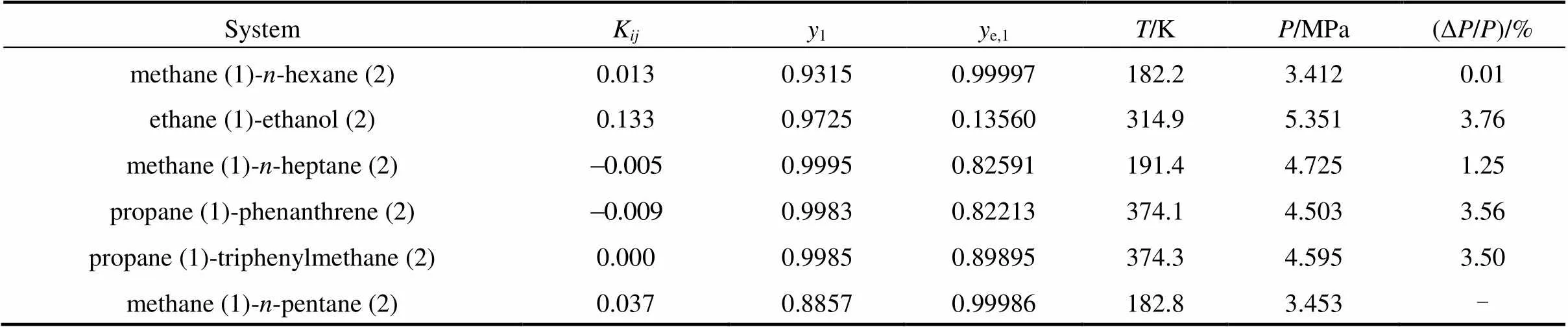
Table 4 The calculation results of critical endpoints and comparison with experimental data

The developed algorithm is also applied to calculate the critical points of complex multiple components mixtures. For ternary systems, the degree of freedom is one according to the phase rule. A line composed of critical endpoints with different compositions is obtained. For the ternary system of carbon dioxide--butanol-dodecane, the interaction parameter for carbon dioxide and dodecane and that for-butanol and dodecane are 0.079 and 0.015, respectively, by using the above technique to fit the interaction parameter. The computation results for the ternary system using the PR equation of state and the SRK equation of state [21] are presented in Fig. 1.

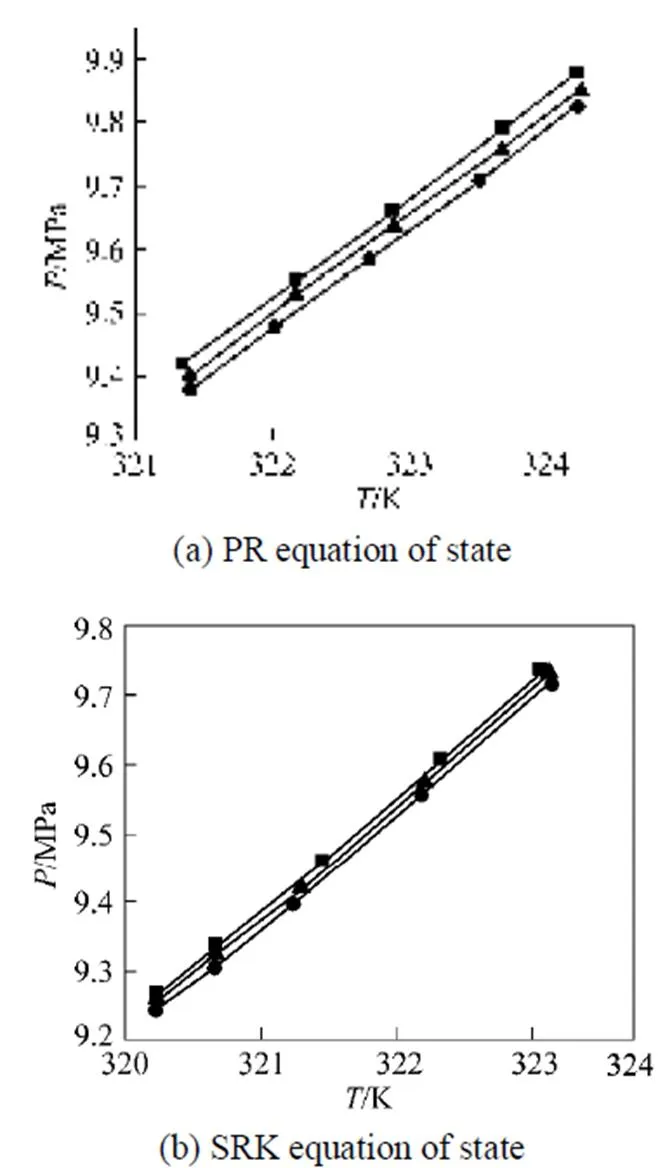
Figure 1 The lines of critical endpoints for the ternary system of carbon dioxide--butanol-dodecane

K:■ 0.09;▲ 0.10;● 0.11

In Fig. 1, the lines of critical endpoints show that the pressure decreases with the increase of the interaction parameter for carbon dioxide and-butanol. The pressure at the critical endpoints calculated with the SRK equation of state is less than that evaluated by the PR equation of state. In Tables 3 and 4, the pressures of the computed critical endpoints with the PR equation of state deviate little from the experimental data. Therefore, the PR equation of state is more accurate in computing the critical endpoints compared with the SRK equation of state. Zhu. [3] also stated that for the calculation of liquid phase and the phase behavior at high pressure, the PR equation of state is better than the SRK equation of state.

Figure 2 illustrates the relation of the pressure and the temperature at the evaluated critical endpoints to the component composition. As the composition of carbon dioxide decreases, the pressure and temperature at the critical endpoint increase simultaneously.

Figure 2 The critical endpoints for the ternary system of carbon dioxide (1)--butanol (2)-dodecane (3)

K:■ 0.09;▲ 0.10;● 0.11

5 CONCLUSIONS

In the algorithm for evaluating critical endpoints, the method of Heidemann and Khalil was employed to calculate critical points and a technique for determining equilibrium phase was developed using the tangent plane criterion. The algorithm is stable, converges rather rapidly, and is applicable for the critical endpoints of non-polar, polar and associating mixtures. As a complex and important phase point in phase behavior of mixtures, the critical endpoint can be employed to fit the interaction parameter of mixtures in critical state at high pressures. The error in the calculated pressure is less than 3.8%. The algorithm is also applicable for calculating the critical endpoints of complex multiple components mixtures. For ternary mixtures, the lines composed of critical endpoints with different compositions can be obtained.

NOMENCLATURE

Helmholtz free energy, J

attraction parameter, Pa·m6·mol－2

co-volume (size) parameter, m3·mol－1

ffugacity of component, Pa

Gibbs free energy, J

Kinteraction parameter

number of components

mole number, mol

pressure, MPa

matrix for quadratic term of Δ

qelement of matrix

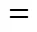
temperature, K

volume, m3

molar volume, m3·mol－1

mole fraction

variables for calculating equilibrium phase

mole fraction

mole fraction

number of moles

variables for calculating equilibrium phase

chemical potential

Subscripts

cal calculation results

e equilibrium phase

exp experimental values

,component indices

t total

1 van Konynenburg, P.H., Scott, R.L., “Critical lines and phase equilibrium in binary van der Waals mixtures”,....,., 298 (9), 495-540 (1980).

2 Peng, D.Y., Robinson, D.B., “A rigorous method for predicting the critical properties of multi-component mixtures from an equation of state”,., 23, 137-144 (1977).

3 Zhu, H.B., Gong, M.Q., Zhang, Y., Wu, J.F., “Review of the research on interaction coefficients used in two cubic equations of state for phase equilibria predictions”,, 5, 7-11 (2005).

4 Michelsen, M.L., “Calculation of critical points and of phase boundaries in the critical region”,., 16, 57-76 (1984).

5 Stryjek, R., “Critical properties of the N2, CH4and C2H6+-alkane mixtures”,., 87 (1), 99-114 (1993).

6 Li, C.C., “Critical Temperature estimation for simple mixtures”,...., 49 (5), 709-710 (1971).

7 Kreglewski, A., Kay, W.B., “Critical constants of conformed mixtures”,..., 73 (10), 3359-3366 (1969).

8 Chueh, P.L., Prausnitz, J.M., “Vapor-liquid equilibria at high pressures: Calculation of partial molar volumes in nonpolar liquid mixtures”,., 13 (6), 1099-1107 (1967).

9 Heidemann, R.A., Khalil, A.M., “The calculation of critical points”,., 26 (5), 769-780 (1980).

10 Michelsen, M.L., “The isothermal flash problem (I) Stability”,., 9, 1-19 (1982).

11 Michelsen, M.L., “The isothermal flash problem (II) Phase split calculation”,., 9, 21-40 (1982).

12 Peng, D.Y., Robinson, D.B., “A new two constant equation of state”,...., 15, 59-64 (1976).

13 Plybon, B.F., “An introduction to applied numerical analysis”, PWS-KENT Publishing Company, Boston (1992).

14 Mehra, R.K., Heidemann, R.A., Aziz, K., “An accelerated successive substitution algorithm”,...., 61, 590-596 (1983).

15 Lam, D.H., Jangkamolkulchai, A., Luks, K.D., “Liquid-liquid-vapor phase equilibrium behavior of certain binary ethane+-alkanol mixtures”,., 59, 263-277 (1990).

16 Lin, Y.N., Chen, R.J.J., Chappelear, P.S., Kobayashi, R., “Vapor-liquid equilibrium of the methane--hexane system at low temperature”,..., 22, 402-408 (1977).

17 Chang, H.L., Hurt, L.J., Kobayashi, R., “Vapour-liquid equilibria of light hydrocarbons at low temperatures and high pressures: The methane--heptane system”,., 12, 1212-1216 (1966).

18 Peters, C.J., Rijkers, M.P.W.M., Roo, D.J.L., Arons Swaan, J.D., “Phase equilibria in binary mixtures of near critical propane and poly-aromatic hydrocarbons”,., 52, 373-387 (1989).

19 Gubblns, K.E., Shlng, K.S., Streett, W.B., “Fluid phase equilibria: Experiment, computer simulation and theory”,..., 87 (23), 4573-4585 (1983).

20 Chen, Z.H., Yao, Z., Huang, Z.M., “Comparison of different mixing rules in the calculation of critical properties for binary mixtures based on PR equation of state”,...., 22 (3), 365-370 (2008). (in Chinese)

21 Luo, M.J., Hu, B., Jiang, T., Xia, S.Q., Ma, P.S., “Analysis and comparison of the alpha functions of SRK equation of state”,..., 16 (5), 766-771 (2008).

2008-12-29,

2009-04-17.

the P&G Corporation.

** To whom correspondence should be addressed. E-mail: yangquan99@mails.tsinghua.edu.cn