An Improved Fuzzy Predictive Control Algorithm and Its Application to an Industrial CSTR Process*

LU Mei (陆妹)**, JIN Chengbo (金成波) and SHAO Huihe (邵惠鹤)



An Improved Fuzzy Predictive Control Algorithm and Its Application to an Industrial CSTR Process*

LU Mei (陆妹)1,2,**, JIN Chengbo (金成波)3and SHAO Huihe (邵惠鹤)1

1Institute of Automation, Shanghai Jiao Tong University, Shanghai 200240, China2Department of Fieldbus, Shanghai Automation Instrument Co., Ltd., Shanghai 200233, China3Department of Product Design, Shanghai GaoKe Valve Manufactory Co., Ltd., Shanghai 200092, China

A finite horizon predictive control algorithm, which applies a saturated feedback control law as its local control law, is presented for nonlinear systems with time-delay subject to input constraints. In the algorithm,free control moves, a saturated local control law and the terminal weighting matrices are solved by a minimization problem based on linear matrix inequality (LMI) constraints online. Compared with the algorithm with a nonsaturated local law, the presented algorithm improves the performances of the closed-loop systems such as feasibility and optimality. This model predictive control (MPC) algorithm is applied to an industrial continuous stirred tank reactor (CSTR) with explicit input constraint. The simulation results demonstrate that the presented algorithm is effective.

predictive control, fuzzy system, time-delay, saturated control law

1 INTRODUCTION

Model predictive control (MPC) has been widely accepted in industry for its ability to handle hard constraints on controls and states. It has, therefore, been widely used in petrochemical and related industries where satisfaction of constraints is particularly important because efficiency demands operating points on or close to the boundary of the set of admissible states and controls. Worst-case infinite horizon predictive control scheme has been studied extensively [1-3].

Time-delays usually exist in practice, especially in process industry. And time-delays can degrade the performances of closed-loop systems and even make the closed-loop systems unstable. Increasing attentions are paid to robust control for uncertain linear time-delay systems [4, 5]. MPC algorithms with a state feedback control law have been proposed [6-9] for uncertain systems with time-delay. A finite horizon state feedback predictive control algorithm for systems with time-delay has been presented [8]. The movement offree control enlarges the feasible set of the system. But it must be solved by a nonlinear quadratic programming problem off-line.

Nonlinear systems always exist in practice and have been studied for a long time [10-12]. Takagi and Sugeno’s (T-S) fuzzy model [13] has been widely used to represent complex nonlinear systems. Several fuzzy model-based predictive control algorithms [14, 15] have been studied, where the issue of transient control performance has been addressed as in general MPC. These strategies of fuzzy model predictive control are actually an extension of the conventional finite horizon MPC. However, their stability and feasibility cannot be explicitly addressed as those in infinite horizon MPC [1-3]. In this article, we extend the idea of worst-case infinite horizon predictive control into the T-S model-based fuzzy predictive controller design.

A finite horizon predictive control algorithm is presented for nonlinear systems with time-delay, applying a saturated feedback control law [16-18] as its local control law. Compared with the algorithm based on nonsaturated local law, the presented algorithm has improved performances including feasibility and optimality. And also the algorithm is easy to be solved by a minimization problem based on linear matrix inequality (LMI) constraints on line. MPC algorithm is applied to an industrial continuous stirred tank reactor (CSTR) with explicit input constraints. The simulation results demonstrate that the presented algorithm is effective.

2 SYSTEM MODEL AND PRESENTATION

2.1 System description

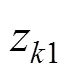
At each time instant, the dynamic fuzzy model (1) can be described as the following global model:

2.2 Problem formulation

The objective of the algorithm is to find the optimal control action subject to constraints:

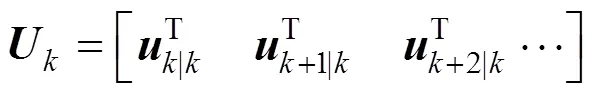
and to minimize the worst case infinite horizon quadratic objective function at each time instant:

2.3 Some preliminaries

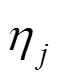
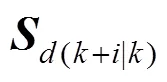
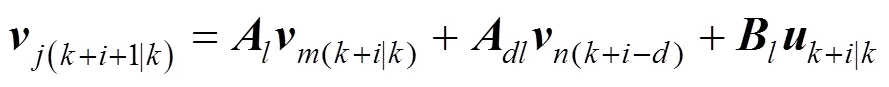
3 MAIN RESULTS

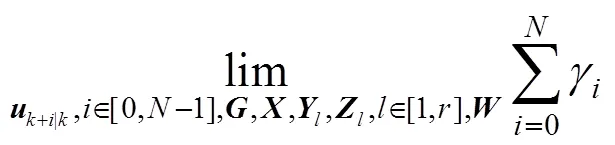
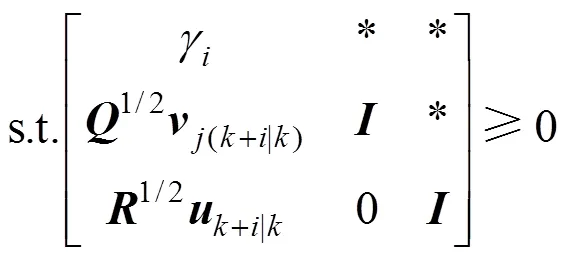
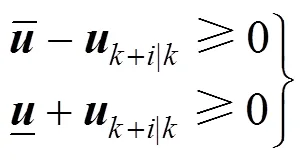
Proof: When the control action (3) is divided into two parts, the infinite horizon quadratic objective can also be divided into two parts:

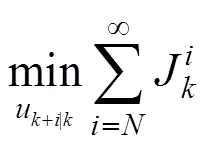
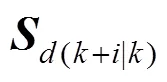
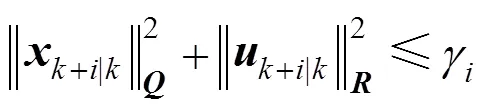
The optimization problem (10) is an infinite horizon min-max optimization problem, so it can not be solved explicitly. Define the following quadratic function:

which satisfies:

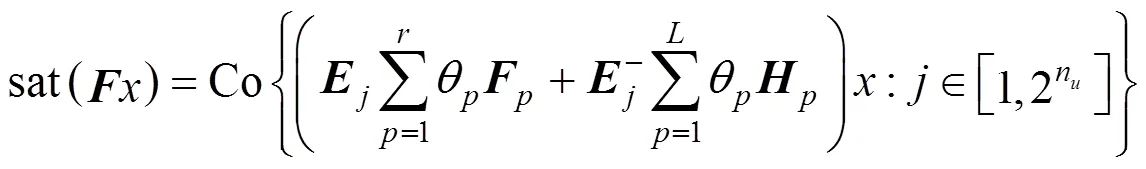
The closed-loop system is described as follows:

When both of the two following inequalities are satisfied, the inequality (13) is satisfied.

The inequality (16) is equivalent to the following inequality:

Apply Schur complementation, the above inequality becomes

Apply Schur complementation, the inequality (19) becomes the LMI (8b).

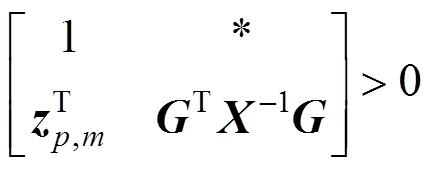
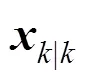
From the inequality (22) and (23), the following inequality is satisfied:

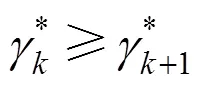
4 CONTINUOUS STIRRED TANK REACTOR

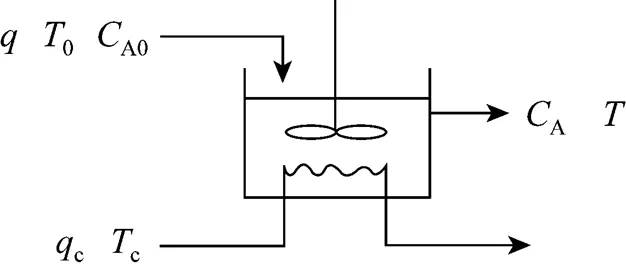
Figure 1 CSTR

The material and energy balance equations are

The above material and energy balance equations are reduced to dimensionless form using the notation:

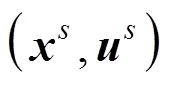
Let the sampling time Δ, the discrete model is given:

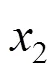
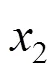
Rule 3: if2is about 4.7052, then

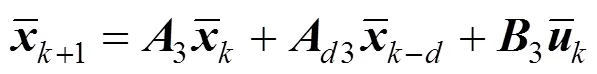
The membership functions are shown in Fig. 2.

Figure 2 Membership functions

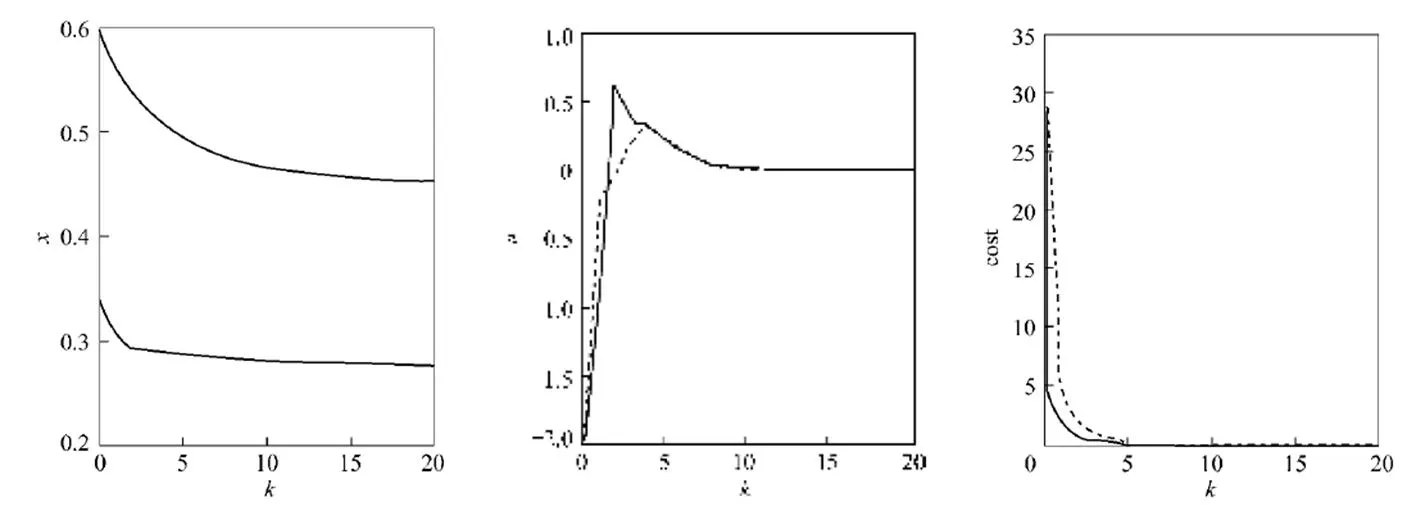
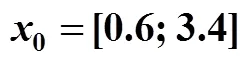
Figure 4 Closed-loop control performance

5 CONCLUSIONS

An improved fuzzy predictive control algorithm applying saturated local control law is presented. It is a receding minimization problem based on LMI constraints. The stability of the presented algorithm is guaranteed as long as the minimization problem is solvable at the initial time instant. And the presented algorithm improves the performances of the controlled systems such as feasibility and optimality. The constrained CSTR problem is considered, the simulation results support the applicability of this algorithm to industrial problems.

NOMENCLATURE

A() concentration of chemical A

A0feed concentration

Co convex hull

specific heat

/ratio of Arrhenius activation energy to the gas constant

0reaction velocity constant

n,ndimension of,

feed flow rate

() reactor temperature

waverage coolant temperature in reactor cooling coil

0feed temperature

heat transfer coefficient times the surface area of reactor

reactor volume

LKLyapunov-Krasovskii function

vert vertex of the convex hull

recycle delay time

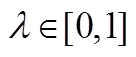
density

1 Kothare, M.V., Balakrishan, V., Morari, M., “Robust constrained model predictive control using linear matrix inequality”,, 32 (10), 1361-1379 (1996).

2 Cuzzola, F.A., Geromel, J.C., Morari, M., “An improved approach for constrained robust model predictive control”,, 38, 1183-1189 (2002).

3 Ding, B.C., Xi, Y.G., Li, S.Y., “A synthesis approach of on-line constrained robust model predictive control”,, 40, 163-167 (2004).

4 Cao, Y.Y., Frank, P.M., “Analysis and synthesis of nonlinear time-delay systemsfuzzy control approach”,.., 8 (2), 200-211 (2000).

5 Cao, Y.Y., Frank, P.M., “Stability analysis and synthesis of nonlinear time-delay systems via linear Takagi-Sugeno Fuzzy model”,., 124, 213-229 (2001).

6 Hu, X.B., Chen, W.H., “Model predictive control for constrained systems with uncertain state-delays”,..., 14, 1421-1432 (2004).

7 Jeong, S.C., Park, P.G., “Constrained MPC algorithm for uncertain time-varying systems with state-delay”,..., 50 (2), 257-263 (2005).

8 Zhang, J., “Study on model predictive control algorithms for time-delay systems”, Ph.D. Thesis, Harbin Univ. of Technology, China (2004).

9 Su, C.L., Wang, S.Q., “Robust model predictive control for discrete uncertain nonlinear systems with time-delay via fuzzy model”,..,, 7 (10), 1723-1732 (2006).

10 Wang, D., Zhou, D.H., Jin, Y.H., “Active fault tolerant control of a class of nonlinear time-delay processes”,...., 12 (1), 60-65 (2004).

11 Bao, Z.J., Pi, D.Y., Sun, Y.X., “Nonlinear model predictive control based on support vector machine with multi-kernal”,...., 15 (5), 691-697 (2007).

12 Zhu, Q.X., Li, C.F., “Dimensionality reduction with input training neural network and its application in chemical process modelling”,...., 14 (5), 597-603 (2006).

13 Takagi, T., Sugeno, M., “Fuzzy identification of systems and its applications to modeling and control”,..,,., 15, 116-132 (1985).

14 Huang, Y.L., Lou, H.H., Gong, J.P., Edgar, T.F., “Fuzzy model predictive control”,.., 8, 665-678 (2000).

15 Mollow, S., Babuska, R., Abonyi, J., Verbruggen, H.B., “Effective optimization for fuzzy model predictive control”,.., 12, 661-675 (2000).

16 Hu, T.S., Lin, Z.L., Control Systems with Actuator Saturation: Analysis and Design, Birkhauser, Boston (2001).

17 Cao, Y.Y., Lin, Z.L., Shamash, Y., “Set invariance analysis and gain-scheduling control for LPV systems subjected to actuator saturation”,.., 46, 137-151 (2002).

18 Limon, M.D., Gomes, S.J.J.M., Camacho, E.F., Alamo, T., “Improved MPC design based on Saturating Controls laws”,.., 11 (2), 112-122 (2005).

19 Jamal, D., Jacques, B., “Parameter dependent Lyapunov functions for discrete time systems with time varying parameter uncertainties”,.., 43, 355-359 (2001).

20 Schuurmans, J., Rossiter, J.A., “Robust predictive control using tight sets of predicted states”,, 147 (1), 13-18 (2000).

2007-08-21,

2008-08-06.

the National High Technology Research and Development Program of China (2004AA412050).

** To whom correspondence should be addressed. E-mail: lumei7718@163.com