勾股定理中的数学思想

王素琴

数学思想，是指现实世界的空间形式和数量关系反映到人的意识之中，经过思维活动而产生的一种结果，它是数学中处理问题的基本观点，是对数学基础知识与基本方法本质的概括，是创造性地发展数学的指导方针。

数学思想是数学解题的灵魂，总结概括数学思想，有利于透彻地理解所学知识，提高独立分析问题和解决问题的能力。现在把冀教版第十六章《勾股定理》一章中体现的数学思想总结如下：

一、整体思想

所谓整体思想是从全题照眼，将数学问题看成一个完整的单位，把数、式、图等各部分综合起来考察，在头脑中构建一个完整的形象，从而抓住问题之间的本质联系，以达到迅捷解题的目的。

例1. 如图（1）在直线L上摆放着3个正方形，斜放置正方形ABCD的面积为1，正放置的两个正方形面积为S₁ ,S₂ ,则S₁ + S₂ =_______。

分析：本题不可能分别求出S₁ ,S₂的值，但可以把S₁+S₂看作整体：AE²+CF²,而通过△AEB≌△BFC可以得到CF=BE，因此S₁+S₂= AE²+BE²,又利用勾股定理知AE²+BE²= AB²=S正方形ABCD =1

二、分类讨论思想

分类讨论是指在解决某些数学问题时，将问题所涉及的所有对象进行分类，然后逐项进行讨论，从而得出正确的解题过程。

例2. 在△ABC中，AB=15,AC=20，AD是BC边上的高，AD=12，求BC的长。

分析：此题没有给出图形，三角形的高可能在三角形的内部，也可能在三角形的外部，因此应分两种情况来求。

解：（1）如图（2）当BC边上的高AD在 △ABC的内部时，在Rt△ACD中，根据勾股定理得：

CD²=AC²-AD²=20²-12²=256∴ CD=16

在Rt△ABD中，根据勾股定理得：

BD²=AB²-AD²=15²-12²=81 ∴BD=9 ∴BC=CD+BD=16+9=25

（2）如图（3）当BC边上的高AD在△ABC外部时，BC=CD-BD=16-9=7，所以BC的长为25或7。

三、转化思想

转化思想是数学思想方法的核心，其它数学思想方法都是转化的手段或策略。如把新问题转化为研究过的问题；把复杂问题转化为简单问题；把实际问题转化为数学问题，最终达到解决问题的目的。

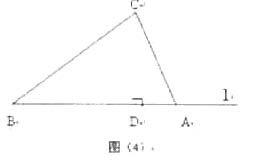
例3.如图（4）在公路l旁有一块山地正在开发，现有C处需要爆破，C与公路停靠站A的距离为300m，与公路上的另一停靠点B的距离为400m，且CA⊥CB，爆破点C周围250m范围内不得进入，问在进行爆破时，公路AB段是否有危险，需要暂时封锁吗？

分析：要判断公路AB段是否需要封锁，只需转化成为C到公路l的距离，若这个距离大于250m，则不需封锁，若小于250m，则需封锁。

解：作CD⊥AB于D

在Rt△ABC中，根据勾股定理得：AB²=BC²+AC²=400²+300²=500²

∴AB=500

根据三角形的面积相等，得：12 AB•CD = 12 BC•AC

即 12 ×500•CD=12 ×400×300

∴CD=240(m)

∵ 240＜250∴公路AB段有危险，需要暂时封锁。

四、数形结合

数形结合是指抽象的数学语言与形象直观的图形结合起来，从而实现由抽象向具体转化的一种思维方式。数学家华罗庚说得好：“数形结合百般好，隔离分家万事休，几何代数统一体，永远联系莫分离。”

例4.在一棵树的10m高处有两只猴子，一只猴子爬下树，走到离树20m处的池塘处，另一只猴子爬到树顶后直接跃到池塘处，距离以直线计算，如果两只猴子所经过的距离相等，求这棵树高。

分析：结合题意画出图（5）可直观看出两只猴子所走路径分别为AB+BC和AD+DC，然后根据勾股定理，构造方程即可解决问题。

解：如图（5）由题意知AB=10m，树BD到池塘C的距离为20m。

设AD=xm,∴DC=(30-x)m

在Rt△BDC中，根据勾股定理得：

BD²+BC²=DC²

即（10+x）²+20²=(30-x)²

解得x=5

∴BD=AB+AD=10+5=15(m)

因此这棵树高15m 。