磨刀不误砍柴工

郑小青

摘 要：课堂教学中引导学生主动参与，探索知识的形成、规律的发现、问题的解决等过程，对学生数学能力的形成，发展创造思维能起到很大的促进作用。

关键词：小学数学；3的倍数特征；教学片断；反思

中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2009）02-0047-02

“磨刀不误砍柴工”这是一句千年古训。课堂教学中引导学生主动参与，探索知识的形成、规律的发现、问题的解决等过程就是“磨刀”的过程。这种教学尽管会耗时较多，但它对于学生形成数学的整体能力，发展创造思维有极大的好处。现以教研课《3的倍数的特征》（人教版数学教材第十册P19）为例，共同探究。

［教学片断］

一、回顾预习，提出任务

师：经过预习，你知道了什么？

生1：一个数各位上的数的和是3的倍数，这个数就是3的倍数。（板书）

师：我们用这个方法来验证一下369和265是不是3的倍数。（生验证）

生2：为什么“一个数各位上的数的和是3的倍数，这个数就是3的倍数”呢？

师：今天我们就研究这个问题。

二、引导探索，知识建构

1.研究整十、整百的数是不是3的倍数。

师：观察黑板上这些数（见图1），哪些是3的倍数？

生1：3、30、300、6、60、600、9、90、900。

师：这些数有什么特点？

生1：最高位上的数是3的倍数。

师：4÷3，5÷3等于多少？

生2：4÷3=1余1，5÷3=1余2。（板书，并让学生计算剩余的数）

师：观察上面的这些算式，你觉得什么地方一样，什么地方不一样？

生3：商不一样。就像分东西一样，东西多，分的人一样，分得的数量就多。

生4：不是3的倍数的数，余数都是1或2。

师：我们以7、70、700这样的数除以3，余数都是几？

生5：余1。

师：像这种整十、整百的数，不管7在什么数位余数都是余1。

生6：老师，我发现了：70÷3、700÷3的余数与个位、十位上的零没有关系，只与最高位上的7有关系，7÷3的余数是1，它们的余数也是1。

生7：是的，判断“整十、整百的数是不是3的倍数”只要看最高位的数是不是3的倍数就行了。

师：说得真好。你能判断8、80、800除以3，余数是多少吗？

（……教师引导，一一擦去上面的算式，板书最后只剩下图2左边的第一列算式。）

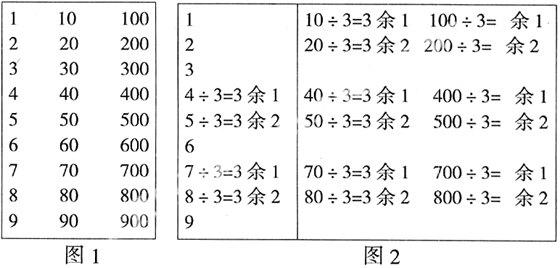
2.研究非整十、整百、整千的数是不是3的倍数。

师：42这个数是不是3的倍数？

生1：是，因为4+2=6，6÷3=2。

生2：4除以3余1，多下来的1个与2合起来是3，3正好是3的倍数。

师：为什么多下来的1个与2合起来是3，这个数就是3的倍数？

生2：多下来的1是1个10，10+2=12，当然是3的倍数啊。

师：48呢？（生答略）

师：621是不是3的倍数。

生3：是，6+2+1=9，9÷3=3。

生4：直接用621÷3=207。

生5：6÷3=2，21÷3=7。

生6：621百位上的6是3的倍数，划去；十位上的2加个位上的1正好是3，3是3的倍数，划去1和2；这样621是3的倍数。

生7：我明白他的意思，6个百是3的倍数，2个十不是3的倍数，但20+1=21就是3的倍数了；所以621是3的倍数。

师：你说得真好。那么这几种方法你们最喜欢哪种？（生答略）

师：702451是不是3的倍数？

生8：我是把各位上的数加起来，7+0+2+4+5+1=19，不是3的倍数。

生9：我是直接计算的，702451÷3=234150…1，不是3的倍数。

生10：702451

↓ ↓↓↓ ↓ ↓

1 2121

7÷3多1，2多2，4÷3多1，5÷3多2，1多1，1+2+1+2+1=7，不是3的倍数。

生11：我用划的方法，7+2=9划去，4+5=9划去，剩下1，不是3的倍数。

师：学到现在，你想说什么？

生12：我觉得生11的方法最好，什么时候都可以用。（大家赞成）

三、巩固练习，解决问题

1.比眼力，判断下面的数是不是3的倍数。

（1）9 生1：是。

（2）4 生2：不是。

（3）421生3：不是。

生4：这个数改为420就是3的倍数了。

生5：还可以把0改成3、6或9。

7+8=15，是3的倍数，划去；5+4=9，是3的倍数，划去；6是3的倍数，划去；7+2=9，是3的倍数，划去；8+5=13，不是3的倍数，所以这个数不是3的倍数。

师：看来我们判断一个数是不是3的倍数，不一定要把所有的数字加起来除以3，数字多时用这种方法更简便。

2.在□里填上一个数字，使这个数有约数3。

（1）63□（2）45□（3）5□6

3.完成书本第19页“做一做”第1、2题。

教学反思：

一、宝剑锋从磨砺出，梅花香自苦寒来

本课教学中教师引导学生经历了“粗磨、细磨、精磨、试刀”四个层次的教学。

1.粗磨。开始阶段，教师充分相信学生，让学生通过课前预习得出“一个数各位上的数的和是3的倍数，这个数就是3的倍数”的特征，并用“369和265”这两个数进行验证。

2.细磨。为什么一个数各位上的数的和是3的倍数，这个数就是3的倍数呢？教师引导学生研究了“整十、整百、整千的数是不是3的倍数”只与最高位上的数有关系，最高位上的数除以3有余数，这个数就有余数。

3.精磨。教师让学生探究了42、48、621、702451等数是不是3的倍数，使学生明白了“非整十、整百、整千的数是不是3的倍数”的算理。

4.试刀。正是因为前面到位的“磨刀”过程，所以当练习“判断785647285是不是3的倍数”时，学生能快速地用“划去”的方法判断，当让学生“在5□6的□里填上一个数字，使这个数有约数3”时，学生也是先“划去”6，再把5加1、或加4、或加7的方法得出正确的答案。

二、问渠哪得清如许，为有源头活水来

教学中，学生可以非常顺利地接受2、5、3的倍数的特征。可有的学生却总爱问：为什么判断2、5的倍数只看个位就行，而判断3的倍数为什么不看个位，却要看各位上的数字之和呢？也就是说学生强烈地需要知道为什么同样是解决“是不是一个数的倍数”的问题，却采用了不同方法。学生的这一困惑促使我进行理性思考：2、5、3的倍数的特征之间应该存在着知识间的“本源一致性”。这是因为：①数是由数字与数位结合后构成的。如42是由数字4在“十位”和数字2在“个位”而构成的。②每个数位只能出现0、1、2、3、4、5、6、7、8、9这10种情况。③最高位为0是没有意义的，遇到数中间或者末尾有0，我们规定0除以2、3、5视为整除。为此设计“3的倍数的特征”的教学新思路。

【责任编辑 高洁】