网络编码在网络安全中的应用

杨义先　郭　钦

摘要：网络编码的思想在1999年由杨伟豪和张珍首次提出，由Ahlswede等人进一步发展和扩充，安全的网络编码也随即提出。蔡宁和杨伟豪首先针对单信源有向无圈网络给出了安全网络编码的定义和模型，其他研究者也各自提出了不同的安全模型，如J P Vilela提出了轻量级安全的网络编码，K Bhattad提出了弱安全的网络编码等，另外还有抗拜占庭攻击的网络编码。网络编码理论亦在网络纠错中得到了应用，杨伟豪和蔡宁推广了经典纠错码, 引入了网络纠错码，杨胜豪在杨伟豪和蔡宁研究的基础上, 研究了线性网络编码的重量性质。 关键词：网络编码；线性网络编码；拜占庭攻击；网络纠错码

Abstract: The concept of network coding was first introduced by R W Yeung and Z Zhang in 1999. It was fully developed by Ahlswede et al. Later secure network coding was introduced, and N Cai and R W Yeung developed the concept and model of secure network coding for directed acyclic network. But for different specialties people gave different models for secure network coding. For instance, J P Vilela introduced light weight secure network coding, and K Bhattad introduced weakly secure network coding. When considering the practical secure network, we must think over the network coding that resists active attack, that is to say resists Byzantine attack. In this paper we also introduce such kind of network coding. On the other hand, researchers have lots of results in network error correction using network coding. R W Yeung and N Cai firstly generalize results in classical error correction codes and bring forward the network error correction codes to correct the errors of transmission; later, S H Yang develops weight characters of network error correction for linear network coding.

Key words: network coding; linear network coding; Byzantine attack; network error correction coding

网络编码的思想建立在网络信息流的基础之上，它通过允许网络节点对来自不同链路的信息进行编码组合，使其既能实现传统路由的存储-转发功能又能实现对信息的处理。[1-5]

1 网络编码理论提升网络容量

网络编码能够提高传输速率，从而达到网络多播的最大流限，并且多播容量等于从信源到信宿节点的最大流的最小值。

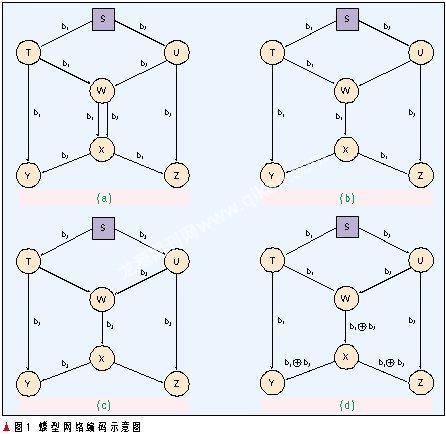
图1所示的蝶型网络是通过网络编码实现多播最大容量的经典例子，也正是通过与传统网络路由进行比较体现了网络编码的优越性：图1(a)中路WX需要两倍的带宽，或者为了使得X和Z都得到信息b1和b2但不增加路WX的带宽，只有平均传送1.5次。信源节点S要多播信息给节点Y和Z。假设每条链路的容量都是1 bit，由最大流最小割定理，S每单位时间可以多播2 bit信息，而按一般的存储－转发模式，不能达到同时多播2 bit信息。因为从图1中可以看出，链路WX每次只能传送1 bit，要传送2 bit信息，就必须使用2次，如图1(b)和图1(c)；这样，经过两次传输，Y和Z分别收到3 bit信息b1、b2和b3。所以网络传输每单位时间至多为1.5 bit。图1(d)采用了网络编码的方法，这样S每单位时间可以多播2 bit信息。但是如果我们不在网络节点W进行编码的话，并且想达到同时多播两个消息给Y和Z两个接受节点的话，我们必须增加WX链路的容量到2，见图1(a)。在本例中，采用网络编码使得每条链路只使用了一次，这样不仅使得网络负载比较均衡，节省了传输次数同时又减小了网络时延，增大了网络吞吐量。如果网络中所有节点对其输入信息进行线性操作，则称为线性网络编码，否则称为非线性网络编码。如果网络节点对信息进行操作的系数是随机选取的，则称为随机网络编码；如果网络节点对信息是通过算法确定出来，则称为确定性网络编码。

2 网络编码理论在数据安全领域的应用

在目前的网络通信中，搭线窃听、拜占庭攻击是破坏数据安全传输的常见(网络纠错)手段和方法。在网络编码出现以前，主要利用作为信息安全的核心技术——密码学领域中的诸如数据加密、哈希函数和消息认证等方式来确保数据的安全传输。然而传统的密码学方法存在一定的局限性，如计算复杂度较大、数据传输速率较低、消息冗余较大等，因此需要寻找一些安全、高效的数据传输方式。虽然网络编码的初衷在于提高网络的吞吐量，但是随着进一步研究发现它也是一种安全网络传输的好方式。然而在抗击拜占庭攻击时，我们不仅要能够检测出敌手对信息的恶意攻击，还要尽量能够做到对这些信息的恢复，这就是网络纠错码。杨伟豪和蔡宁首先提出了网络纠错码的概念和理论框架。

2.1 抗搭线窃听的网络编码

蔡宁等人最先研究了单信源有向无圈网络中数据安全多播问题[3]，给出了搭线窃听的网络通信模型，并且构造了在信息论意义下的安全网络编码，即窃听者无论偷听所给定偷听范围内的哪个窃听集都无法恢复出原始信息。如图2所示，从信源发出的信息中，m是消息本身，而k是为了达到安全的随机数。图2中红线是窃听集，但是一个时间内只允许敌手窃听其中的一条，这样接收节点T和T＇能够安全接收到信源传来的消息ｍ。

Feldman等人[6]在文献[3]的基础上证明了将线性网络编码变为安全网络编码，等价于找到满足一定广义距离性质的线性码，并说明如果放弃少量的整体容量，就可以在较小的基域上构造出安全的网络编码。K Jain等人[7]在文献[3]的安全性假设下, 得到了单源网络中(可以有环)以单位速率安全单播的充要条件，在假定搭线窃听者具有有限计算能力的情形下，利用Hash函数和网络编码相结合的方法，使得网络以更高的速率传输数据，而搭线窃听者得不到信源的任何有用信息。K Bhattad等人[8]针对无圈网络多播问题，提出了搭线窃听者不能得到任何有意义信息的弱安全网络编码模型，其体系较简单，虽不是理论上的信息安全，但也有一定的适用范围。(它与文献[3]中一般的信息论意义下的安全性的差别在于：前者是指窃听者不能得到有关一个信源发出的任何部分消息，而后者的安全指的是不能得到由任何信源发出的所有消息，其本质的差别就在于整体相互独立强于部分相互独立)。T Chan 等人[9]讨论了多源安全网络通信问题，在一定的窃听范围的限制下，利用随机网络编码的方法，给出了多源安全网络编码容量的内界、外界和线性规划界，它们推广了杨伟豪所得到的相关结论。

2.2 抗拜占庭攻击的网络编码

网络编码在抗搭线窃听方面得到广泛研究的同时，很多研究者又开辟了网络编码在针对抗击另外一种有更大安全隐患的拜占庭攻击的研究。在这种攻击问题中，攻击者不仅想得到一些有用的消息，还通过多种手段来阻止通信双方的正常通信，即加入或修改正常传输中的信息。随着对安全、高效的数据通信的要求越来越高，这种恶意的攻击问题的解决势必越来越重要。

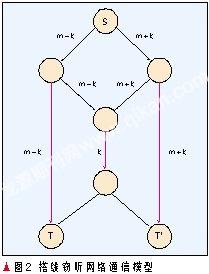
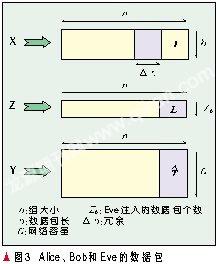
图3是有线和无线网络的带有拜占庭攻击者的攻击模型，为了简化符号，只考虑单信源单信宿的通信问题。相似于许多网络编码的算法，这里每个体制都可以从单个接收方的情形推广到多播通信。在网络编码情形下，有拜占庭攻击的一般通信模型，可从两个方面来描述：攻击模型和网络与网络编码模型。下面主要基于S Jaggi等人[10]提出的有关结果。

图3中X表示Alice发出的原始消息块，Z表示攻击者Eve注入的错误消息块，Y表示经过篡改被Bob接收的消息块。矩阵I、L和T分别表示数据包X、Y和Z的编码向量。

信源Alice和信宿Bob通过一个有线或无线网络通信，攻击者Eve隐藏在网络中。此时在上面普通通信模型基础上有两个改变：一是信宿由于受到攻击者的影响将作如下更改，即信宿Bob收到的数据包所组成矩阵Y的列秩变为b +c 0，其中c 0是从Eve到Bob的最小割值。Bob试图利用他所收到的数据包所构成的矩阵Y，排除错误、重建Alice发出的信息X；二是在通信过程中有了存在攻击者Eve的攻击，将影响中间节点的编码和传输。假定恶意数据包是附加在信源数据包后的一部分，令c 0×n阶矩阵Z表示Eve 注入到每组中的信息，它的第i 行Zi表示第i 个恶意的信源数据包。当Eve注入自己的数据包时，将这些修改后的数据包假装成从Alice到Bob传输的信息流的一部分。Eve是非常强大的，有极大的计算能力，知道Alice和Bob之间的编码和解码体制，也知道在内部节点处所执行的网络编码，并且知道确切的网络实现。

针对攻击者的不同攻击能力可以分为如下3种主要攻击模型。

(1)秘密共享模型

此模型假定Alice和Bob有一个低速率的秘密信道，Eve不知道秘密信道上的传输消息。考虑将消息经过网络编码后在网络上传输，Eve可以观察到所有除秘密信道之外的所有传输，也可以选择是否在他所控制的节点处在要传输的数据包中注入一些恶意数据到从而达到阻止Alice和Bob通信的目的。

(2)万能攻击者模型

此模型中Eve除了在控制链接数目上受到一定限制外，是万能的、无所不知的，Alice和Bob之间没有独立于Eve的秘密信道。假设攻击者到接收节点之间的最小割c 0＜C /2，其中C是网络容量。

(3)有限的窃听模型

在这个模型中，Eve 的窃听能力是有限制的，只能观察到至多Z I个传送的包。

2.3 适应网络纠错的网络编码

在网络编码先前的研究中，网络中的传输多数情况下是假定无差错的。然而，实际的通信网络中，传输受各种不同错误的影响，例如：

由信道噪声引起的随机错误。在经典纠错码理论中已经广泛讨论了随机错误的纠正，在一个数据包中可以利用具有好的错误检测能力的纠错码作为局部码，当数据包中错误的数目很少时错误可以被纠正，而当错误很大时能以很高的概率检测出错误、并删除数据包，只有在错误不可检测的情况下错误包依然保留在网络中，并且当使用网络编码时会影响其他的数据包。

擦除错误或者由网络拥塞引起的数据包丢失。这种类型的错误在网络理论中被广泛讨论，数据包丢失也可能是由数据包头的错误引起。

由恶意节点故意改变或者创造的数据包。恶意节点的目的是在网络中干扰通信，并且使通信不可靠。这或许可能是网络通信较其他类型错误更严重的问题，恶意节点可能改变数据包携带的消息或者是包含在数据包包头的信息。

包头错误。在一个数据包中，一些重要的信息例如在网络编码中的全局编码核、数据包产生的位置(信源)、数据包的目的地(接收节点)等是记录在包头中的，包头任意错误可能引起传输的严重问题。如果全局编码核改变，称为是全局编码核错误，将影响接收节点的解码；如果目的地的信息被改变，可能引起接收节点的数据包丢失。而按Lamport等人[11]的分类，上面的大多数错误都可归结到拜占庭错误中。

在研究网络编码理论的同时，一些研究者已经注意到网络编码可以用来检测和纠正网络中的错误。杨伟豪和蔡宁[12-13]在经典纠错码基础上，引入了网络纠错码的概念。此推广目的在于利用网络编码，通过引入空间域的冗余代替时间域的冗余来纠正网络通信中的错误。他们将经典纠错码的Hamming界、Singleton界和Gilber-

Vashamov界推广到网络编码，并构造纠正错误能力能达到Singleton界的极大距离可分码(MDS码)，以及提出了网络纠错码的解码原则——包括接收节点处的解码矩阵和错误空间、接收节点处的消息空间、错误模式的秩、网络纠错码的最小距离等。

杨胜豪[14]在杨伟豪和蔡宁的基础上，研究了线性网络编码的重量性质。在为差错向量、接收向量和信息向量引入了一些新的称为网络重量的定义的基础上(所有这些网络的Hamming重量在特殊的网络纠错码情形下，就变为通常的Hamming重量)，定义了网络编码的最小距离。

D Silva等人[15]主要考虑端到端的错误控制编码，受R Koetter and Kschischang[16]的启发，致力于实际码的构造。不像张珍和杨伟豪提出的网络编码差错控制方式，D Silva假定信源和接收节点未知，或者至少不设法知道网路拓扑或者网络中所使用的特定的网络编码，传输器选择对信息编码合适的向量空间V，而不是传统纠错码中的向量。V 的选择是通过将V 的一组基嵌入到网络中以发出信号，其中每个基向量都对应一个传送的数据包，接收者搜集数据包。假设这些数据包能构成一个接收空间U的一组基，如果V ∩U 可得一个充分大维数的空间，那么正确接收是可能的。通过在子空间上定义一个合适距离，就可以一般化在汉明距离意义下的经典编码理论。此方法在任意给定域和对数据包大小无实质上要求的情况下都可行，对于一大类码，R Koetter and Kschischang[16]的子空间距离度量和秩度量的是密切相关的，许多来自秩距离码理论中的工具可以运用到随机网络编码。在秩距离码的环境下，错位和错值两种情形可能发生——错位对应于知道错误的位置但不知道错误的值，错值意味着知道错误的值但不知道错误的位置，这些概念推广了在秩距离情形下行列错误术语。

张珍在杨伟豪和蔡宁研究的基础上，致力于线性网络纠错码基本问题的研究提出了线性网络纠错码的基本性质、构造和对各种各样错误的差错纠正能力[17-18]。文中的讨论限制在单信源的多播情形，作者定义了一个网络纠错码的最小距离，它和经典编码理论中的最小距离起同样的作用。基于杨伟豪和蔡宁提出的网络纠错码的解码原则，作者引进两个解码算法并且分析它们的性能，进而阐明了全局核错误和擦除错误纠正问题，并利用码的最小距离来刻画此类型错误的差错纠正能力。

3 结束语

网络编码在抗搭线窃听、抗拜占庭攻击和网络纠错码等网络安全领域的3个重要方面已展开应用，但是还需进一步发展[19]，例如网络编码在抗搭线窃听方面研究的假设还是稍微有些强，所以将这些理论应用到现实网络通信中还有很多工作要做。

4 参考文献

[1] YEUNG R W, ZHANG Z. Distributed source coding for satellite communications [J]. IEEE Transactions on Information Theory, 1999, 45(3):1111-1120.

[2] AHLSWEDE R, CAI N, LI S Y R, et al. Network information flow [J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204-1216.

[3] CAI N, YEUNG R W. Secure network coding [C]//Proceedings of 2002 IEEE International Symposium on Information Theory (ISIT 2002), Jun 30-Jul 5, 2002, Lausanne, Switzerland. Los Alamitis, CA, USA: IEEE Computer Society, 2002: 323.

[4] TAN J, MEDARD M. Secure network coding with a cost criterion [J]. Proceedings of 4th International Symposium on Modeling and Optimization Modeling Mobile, Ad Hoc and Wireless Networks (WiOpt'06), Apr 3-6, 2006, Berlin, Germany. 2006: 6p.

[5] VILELA J P, LIMA L, BARROS J. Lightweight security for network coding [C]// Proceedings of the IEEE International Conference on Communications (ICC08), May 19-23, 2008, Beijing, China. Piscataway, NJ, USA: IEEE, 2008: 1750-1754.

[6] FELDMAN J, MALKIN T, STEIN C, et al. On the capacity of secure network coding [J]. Proceedings of 42nd Annual Allerton Conference on Communication, Control, and Computing, Sep 29-Oct 1, 2004, Monticello, IL, USA.

[7] JAIN K. Security based on network topology against the wiretapping attack [J]. IEEE Wireless Communications, 2004, 11(1):68-71.

[8] BHATTAD K, NARAYANAN K R. Weakly secure network coding [C]// Proceedings of First Workshop on Network Coding, Theory, and Applications (NETCOD05). Apr 2005, Riva del Garda, Italy. 2005.

[9] CHAN T, GRANT A. Capacity bounds for secure network coding[C]// Proceedings of Australian Communications Theory Workshop (AusCTW 2008), Jan 30-Feb 1, 2008, Christchurch, New Zealand. Piscataway, NJ, USA: IEEE, 2008: 95-100.

[10] JAGGI S, LANGBERG M, KATTI S, et al. Resilient network coding in the presence of Byzantine adversaries [C]// Proceedings of 27th IEEE International Conference on Computer Communications (INFOCOM07), Mar 6-12, 2007, Anchorage, AK, USA., Piscataway, NJ, USA: IEEE, 2007: 616-624. [11] LAMPORT L, SHOSTAK R, PEASE M. The Byzantine generals problem [J]. ACM Transactions on Programming Languages and Systems, 1982, 4(3): 382-401.

[12] YEUNG R W, CAI N. Network error correction, part I: Basic concepts and upper bounds [J]. Communications in Information and Systems, 2006, 6(1):19-36.

[13] CAI N, YEUNG R W. Network error correction, part II: Lower bounds [J]. Communications in Information and Systems, 2006, 6(1):37-54.

[14] YANG S, YEUNG R W. Characterizations of network error correction/detection and erasure correction [C]// Proceedings of Third Workshop on Network Coding, Theory, and Applications (NETCOD07), Jan 2007, San Diego, CA, USA. 2007.

[15] SILVA D, KSCHISCHANG F R, KOETTER R. A rank-metric approach to error control in random network coding [J]. IEEE Transactions on Information Theory, 2008, 54(9): 3951-3967.

[16] KOETTER R, KSCHISCHANG F R. Coding for errors and erasures in random network coding [C]//Proceedings of 2007 IEEE International Symposium on Information Theory (ISIT 2007), Jul 24-29, 2007, Nice, France. Los Alamitis, CA, USA: IEEE Computer Society, 2007: 3579-3591.

[17] ZHANG Z. Network error correction coding in packetized network[J]. Proceedings of 2007 IEEE Information Theory Worksho (ITW06), Oct 22-Oct 26, 2006, Chengdu, China. Piscataway, NJ, USA: IEEE, 2006: 433-437.

[18] ZHANG Z. Linear network error correction codes in packet networks [J]. IEEE Transactions on Information Theory, 2008, 54(1): 209-218.

[19] 马松雅, 罗明星, 杨义先. 抗拜占庭攻击的安全网络编码综述[C]//中国电子学会第十五届信息论学术年会暨第一届全国网络编码学术年会论文集. 2008年7月28日至30日, 青岛, 中国. 北京: 国防工业出版社, 2008.

收稿日期：2008-11-15

杨义先，北京邮电大学计算机学院执行院长，信息安全中心教授、博士生导师。研究方向包括信息安全、网络安全、编码密码学、数字信号处理、网络编码等。获得10余项国家级和省部级科技奖励，发表论文500余篇。

郭钦，北京邮电大学计算机学院在读博士研究生，主要从事网络编码和分组密码的研究。