司马老师的讲座
2009-02-16孙维梓
孙维梓
谁都爱听司马老师每周末举办的头脑思维讲座,因为大家可以从中得到不少有关思维方面的启发。
上周末他刚上讲台,就给同学们展示出一幅钟面的图画说:“请看,这是一个钟面,大家肯定司空见惯了。”(图1)

我们发现钟面是被一条线段分隔成为上下两块,但是不明白有什么用,就都睁大眼睛等待着。
只见老师接着说:“钟面已被线段分成了两块区域,分别包含有四个数与八个数。那么这两块的各数之和相等吗?”
这还用问?这十二个数的总和就等于1+2+3+4+5+6+7+8+9+10+11+12=78,而现在线段却把78 分成为10+11+12+1=34 与2+3+4+5+6+7+8+9=44,它们当然不相等。
老师一字一顿地问:“那么,有谁能在钟面上再画一条线段,使上下这两块的各数之和相等吗?”
大家纷纷议论起来,还在纸上左画右画,始终迷惑不解。我们向司马老师提问说:“照我们看,这道题根本无解。钟面上再添画上一条线段,那么分成的区域肯定会不止两块,里面的各数之和怎么可能相等呢?”
可老师说:“谁说本题无解?瞧我做给你们看!”说罢,他拿起笔,就在钟面上的1 字前面又添上了一短竖,使之变成了11,如图2 那样。于是分成的上下两块的各数之和就都成为44 了!老师解释说:“短竖线当然也是一条很短的线段,但你们的头脑由于受到了原有那根线段的影响,总是在潜意识中认为它一定是另外一条横断的线段罢了。”
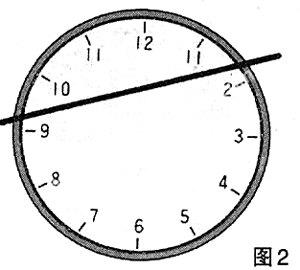
我们全都哑然失笑起来,笑自己的思维怎么会如此容易上当,也体会到所谓“思维创新”真是说说简单做时难啦。
然而司马老师话锋一转,他又说:“同学们已经学过了有理数。那么我要再问问大家,这道题能不能有第二种解法呢?”
这倒奇了,第二种解法?还与有理数有关?我猛然想到:既然老师能把上方区域里的34 设法变成44,从而使上下两块里面的各数之和相等,那么我能不能让下方区域里的44 也变为34,同样也使这上下两块全化为相等的和呢?我大胆地说:
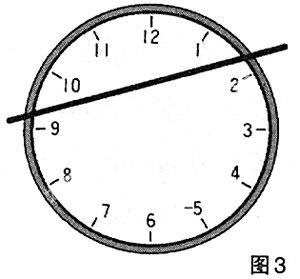
“司马老师,我能不能在下面5的前面再添画上一短横,使它成为(-5)。这样在求代数和的时候,下方区域里的总和就将减少10,它的各数之和不就与上方各数之和都是34了吗?”
我还上去把钟面改成图3 那样,博得了同学们的一片掌声。只见司马老师笑容满面,他赞许地说:“好,好,现在上下两块的各数之和分别是10+11+12+1=34 以及2+3+4+(-5)+6+7+8+9=34了,不也做到相等了吗?要想使两数相等,不但可以设法增大较小的那个数,还可以设法削减比较大的那个数呀。”
原来司马老师今天讲座的目的就是要突破我们头脑中的禁区,使思维不僵化,力求灵活多变呢。
