防渗墙钻孔压水流量与渗透系数关系的近似计算
2009-01-29任大春吴新霞
任大春,吴新霞
1 概 述
垂直防渗墙由于其防渗可靠性好、维护成本低、施工简单、无移民工作等优点,近十年来,已经在江河堤防防渗加固工程中得到越来越普遍的应用。堤防防渗工程中防渗墙的主要技术指标主要包括:混凝土强度、弹性模量、渗透系数、水力坡降以及防渗墙墙面及接缝的平整度、垂直度等。防渗墙施工质量的好坏取决于其抗渗性能的高低,其中防渗墙渗透系数是关系到防渗效果的最重要的指标。
防渗墙渗透系数的检测方法较多,室内方法有机口取样检测、钻孔取芯检测,现场方法有围井试验法、钻孔压水试验法等。采用机口取样和钻孔取芯法检测均有很大的缺陷,机口取样加工成的混凝土试块和钻孔取芯获得的混凝土芯的质量均好于实际情况,不能反映施工工艺所造成的抗渗质量隐患,因而试验的代表性不够。围井法虽然是在现场进行检测,但施工工艺复杂、耗资大、时间长、对施工完成的堤防有一定损伤,而且围井自身的渗透量较难观测,也影响了围井检测的可信度。而防渗墙钻孔压水试验原位检测方法因施工简单、成本低、时间短、对堤防没有损伤,是一种值得推荐的现场检测方法。
岩石力学及混凝土中渗透系数的测试可以按照《水利水电工程钻孔压水试验规程》(SL25 92)执行[1],但堤防上的防渗墙一般较薄,与大体积半无限岩体采用压水试验测试渗透系数的边界条件完全不同。因此,采用规程中推荐的公式和方法与实际情况存在很大的差异。
本文通过饱和非饱和三维渗流计算分析防渗墙钻孔压水试验中渗流分布特性,推导防渗墙钻孔压水试验的渗透系数近似计算公式,为堤坝防渗墙施工质量的快速检测工作提供了一定技术支持。
2 防渗墙钻孔压(注)水渗流场数值模拟计算
2.1 计算模型与分析方法
选取长江干堤防渗墙工程中的2种典型剖面(图1),假定天然地下水位与堤内外地面高程齐平,防渗墙厚40 cm,压水试验钻孔直径11.3 cm,压水试验注水孔位于防渗墙中心,试验段长度6 m,墙两侧地下水位与天然地下水位基本一致。计算方法采用饱和非饱和有限单元法[2]。

图1 长江干堤典型堤段防渗墙工程布置图(单位:m)Fig.1 Layout of the cut-off walls in typicol section of Changjiang River main levce
2.2 计算成果分析
根据上述计算条件进行饱和非饱和有限元数值计算,计算成果见表1和表2。

表1 注水孔中心(顺游向)浸润线分布Table 1 Distribution of saturation of water injecting hole centre along flowdirecction m
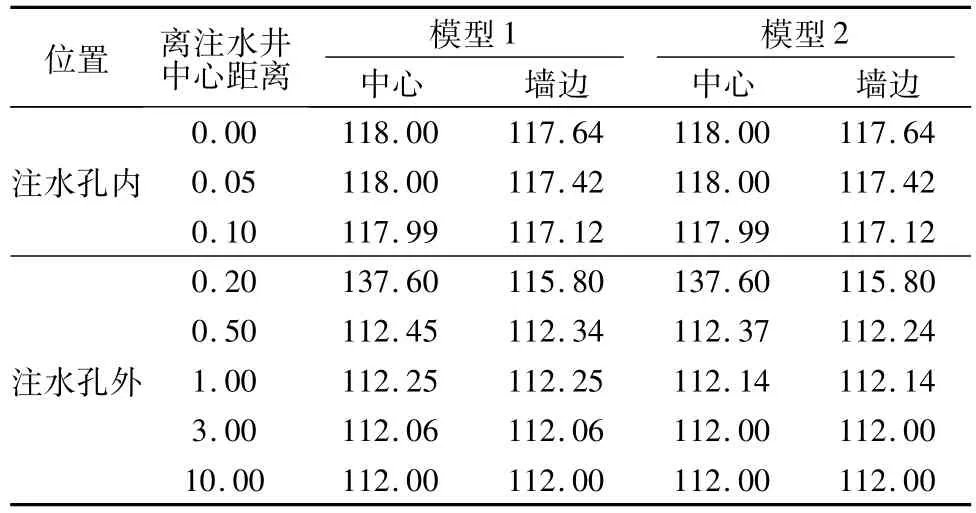
表2 沿防渗墙方向浸润线分布Table 2 Distribution of saturation lines along the cut-off wall direction m
从计算成果可以看出:
(1)防渗墙内注水试验仅对注水点附近局部范围内的天然地下水位产生一定的影响,6 m深的注水孔最大抬高地下水位仅0.47 m,离注水点3 m范围以外基本不受注水影响。
(2)防渗墙内注水点附近水位较高,注水点所在横剖面(顺流向)墙边水位仅降落0.36 m,但由于防渗墙厚度较薄(仅0.4 m),注水对防渗墙内水位的影响主要限于注水点附近0.2 m范围内(即墙厚范围),3 m以外基本不受影响。
(3)当防渗墙透水性与堤身堤基土层透水性相差较大时,堤基透水性的改变对渗流场和渗流量的影响不大。
可见:当防渗墙墙身的渗透系数明显小于堤身渗透系数时,堤基透水性对渗流场和渗流量的改变不大,计算时可以不考虑堤基的影响;防渗墙压(注)水对地下水位影响不大,压(注)水影响范围有限,并且顺流向和顺防渗墙两方向基本相当,因而,可以只在有限范围内考虑其渗流的影响。
2.3 钻孔压(注)水试段长度对渗透系数检测结果的影响
为分析孔压(注)水试验段长度对防渗墙的渗透系数检测结果的影响,对上述模型1取试验段长分别为4 m,6 m和9 m进行渗流计算,3种压(注)水试验段长度的渗流浸润线分布成果列入表3,表4中。进一步比较分析单位压力、单位长度渗流量的变化见表5和图2。
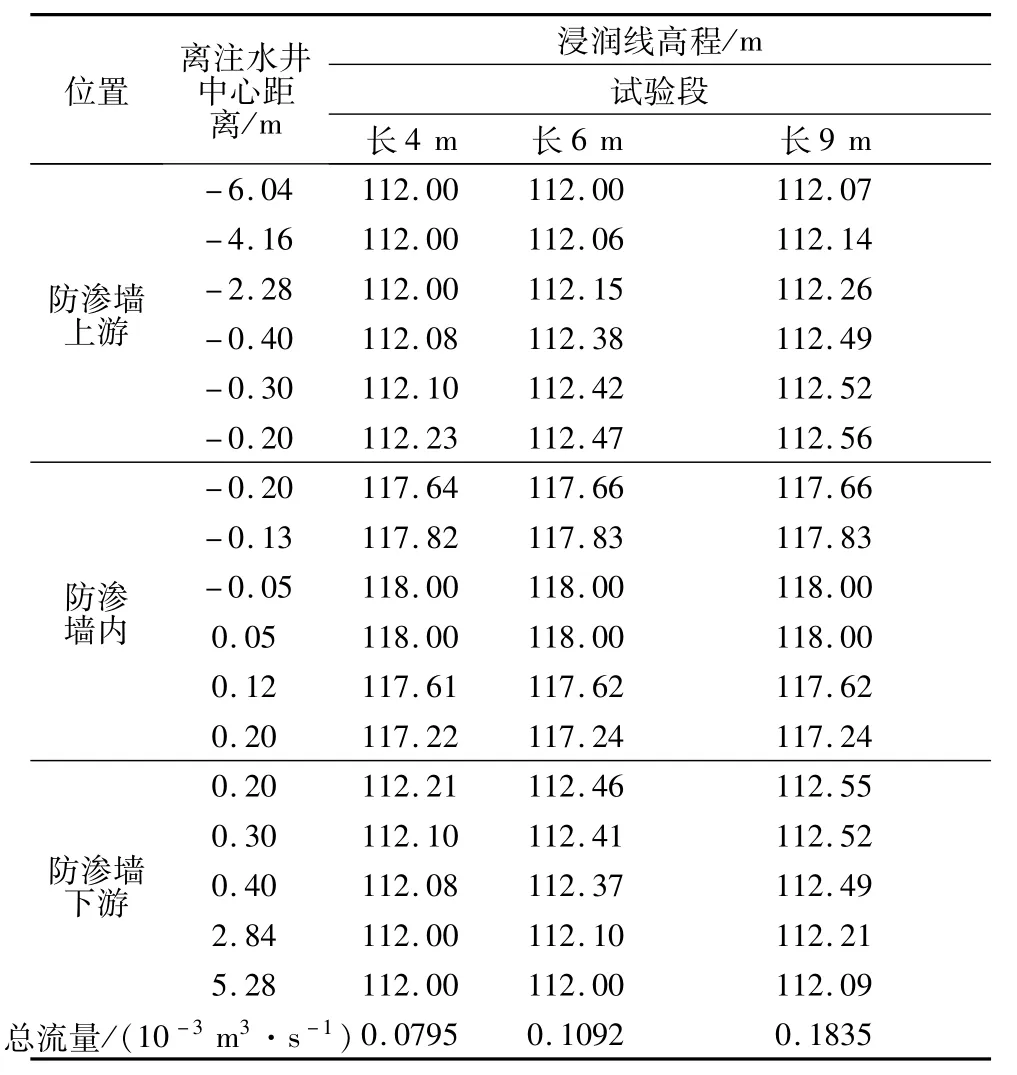
表3 注水中心顺流向浸润线比较Table 3 Comparison of saturation lines of water injecting hole centre along streamflow direction
从计算成果可以看出:压(注)水试验段长度对防渗墙的渗透系数检测结果的影响明显,试验段越短,计算成果的单位流量越大;相应地,由试验检测结果得到的渗透系数将越大。从图2的成果可以看出:试验段足够长时,计算成果的单位流量将趋向稳定;当试验段长度大于6 m后(约53倍钻孔直径),对单位流量的影响很小。
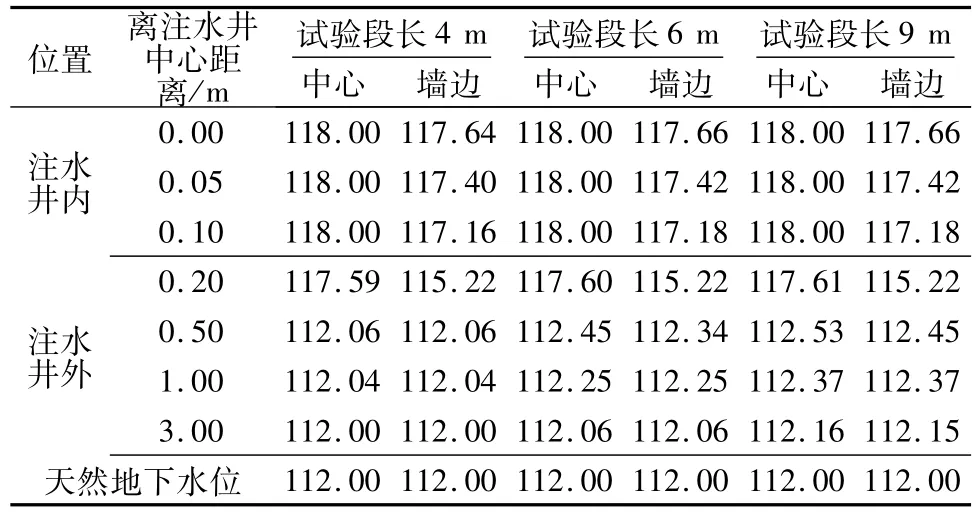
表4 顺防渗墙向浸润线比较Table 4 Comparison of saturation lines along the cut-off wall direction m
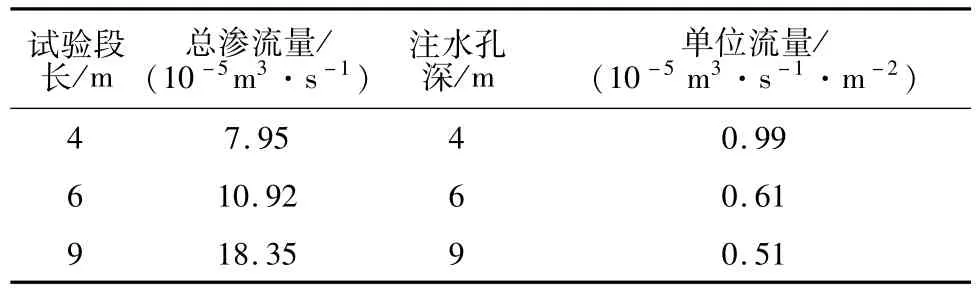
表5 单位压力单位长度渗流量比较Table 5 Comparison of unit permeable dischanges under unit pressure
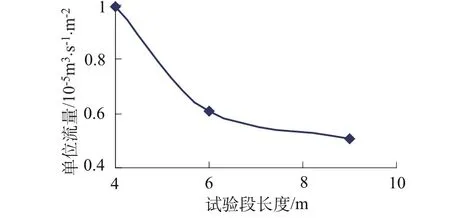
图2 试验段长度与单位流量的关系比较Fig.2 Relationship between length of test section and unit discharge
3 注水量与防渗墙渗透系数之间的近似计算方法
上一节已对防渗墙抗渗性能原位压(注)水试验墙体渗透流量进行了数值计算。数值计算需进行建模并划分网格,计算相对复杂,对某一特定问题进行计算是可行的,但要广泛应用则工作量较大,因此,需寻找一种既简单又可靠的计算方法,即采用简易的近似公式进行计算。图3为墙体注水试验简图。
从第2节的计算成果看,当试验段足够长时(大于53倍钻孔直径),试验段长度对单位流量的影响很小,注水井仅对井附近的渗流场产生一定的影响,影响范围约控制在防渗墙厚度范围内,并在顺流向和顺防渗墙两方向基本相当,因此可以将注水孔渗流场近似地模拟为轴对称渗流场,采用轴对称渗流计算公式近似计算[3-5]:
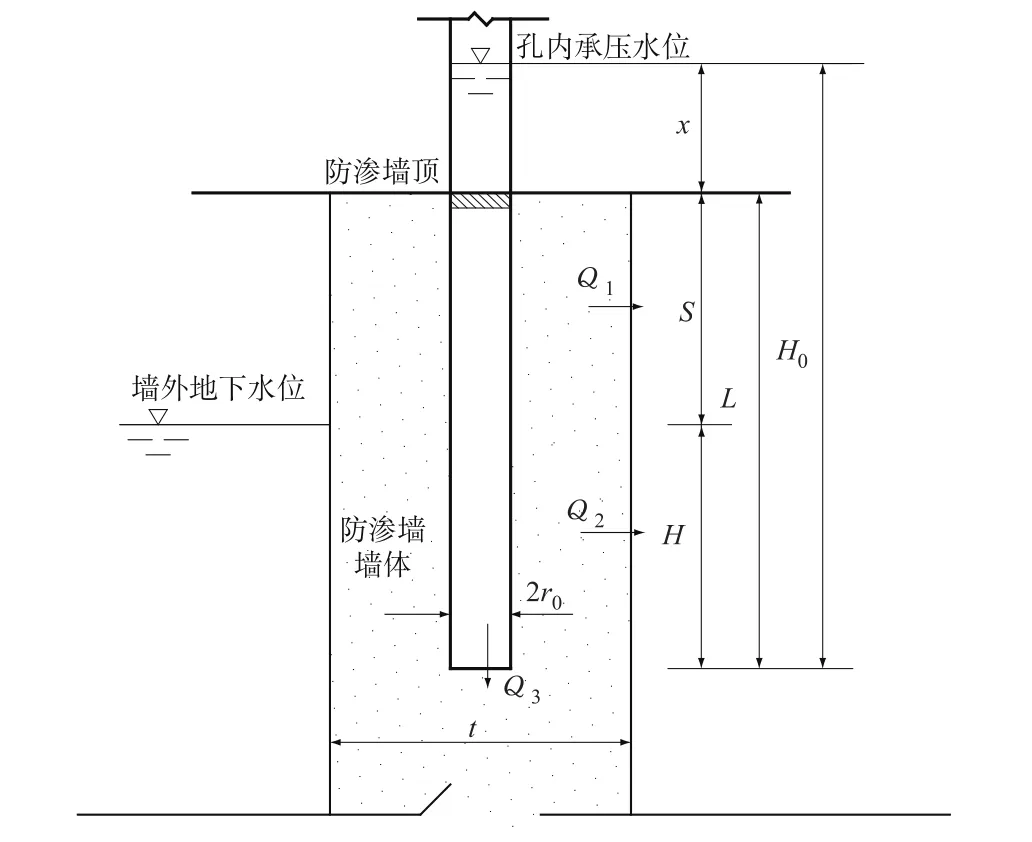
图3 墙体注水试验简图Fig.3 Sketch of water injecting test of the cut-off wall

针对图3的情况,位于墙外地下水位线以上部分的注水井渗流属于有自由面的潜水渗流,其渗流量Q1可按照轴对称潜水渗流公式近似计算:
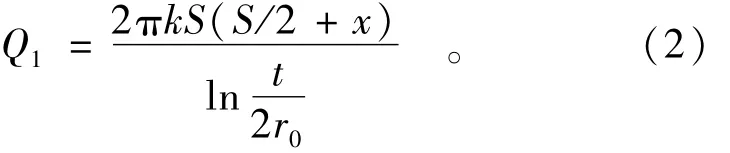
位于墙外地下水位线以下部份的注水井渗流属于承压渗流,其渗流量Q2可按照轴对称承压渗流公式近似计算:

注水井底部的渗流Q3可按照轴对称浅井渗流公式近似计算:
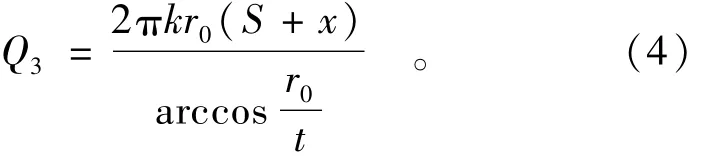
由于注水井井径远小于井深,底部的渗流Q3相对较小,一般可以忽略不计,因此注水井的渗流量可按照下式近似计算:

将(5)式计算结果与表1的数值计算结果进行对比(见表6)可知,公式误差约为18.61%,而且近似计算结果偏小,相应地利用公式反算的注水试验渗透系数略偏大,有利于工程安全,符合一般渗流计算中渗流量的精度要求,可以在防渗墙现场检测中推广应用。

表6 防渗墙注水总渗流量计算成果Table 6 Calculated tutal permenble discharges of water injecting in the cut-off wall 10-5 m3/s
4 结 论
(1)防渗墙注水仅对注水点附近局部范围内的地下水位有一定影响,离注水点3 m范围以外基本不受注水影响。
(2)防渗墙内注水点附近水位较高,注水对防渗墙内水位的影响主要限于注水点附近0.5倍墙厚范围内,3 m以外基本不受影响。
(3)当防渗墙透水性明显低于堤身堤基土层透水性时,堤基透水性的改变对渗流场和渗流量的影响不大。
(4)压(注)水试验段长度对防渗墙的渗透系数检测结果的影响明显,试验段越短,计算成果的单位流量越大。当试验段长度大于约53倍钻孔直径时,对单位流量的影响很小。
(5)利用本文推荐的计算公式反算防渗墙渗透系数的误差约为18.61%,符合一般渗流计算中渗流量的精度要求,而且计算结果有利于工程安全,可以在防渗墙现场检测中推广应用。
[1]SL25 92,水力水电工程钻孔压水试验规程[S].
[2] 任大春,吴昌瑜,朱国胜.三峡二期围堰饱和-非饱和渗流分析[J].长江科学院院报,1997,(2):44-47,56.
[3] 安徽水利科学研究所.多层地基和减压井沟的渗流计算理论[M].北京:水利出版社,1980.
[4] 陈济生.不完整井压力渗流问题的一种近似解[J].水利学报,1980,(4):57-63.
[5] 任大春.不完全井渗流近似计算及其应用[J].长江科学院院报,1990,(3):45-54,60.
