等效裂隙岩体THM耦合并行有限元程序开发
2009-01-29张强林曹国利
张强林,王 媛,曹国利
有限元数值计算是研究岩土工程问题的一种重要方法,由于岩土工程领域研究对象所处的环境越来越复杂,模型考虑越来越多,再加上原本的岩土介质材料非线性,各向异性等计算需要,使得数值计算工作量越来越大,而计算时间也越来越长,如果采用简化模型或粗网格等手段来减少计算量则计算精度会受到影响。计算精度与计算时间之间的矛盾,对于现有的有限元模拟来说是很大的挑战,因此有限元并行计算模拟即成为人们解决此问题的首选方案,如张友良等[1]、茹忠亮等[2]针对水布垭地下厂房的研究,刘耀儒等[3,4]针对二滩、锦屏等工程研究都是针对单场进行并行计算,Wang等[5]、江春波等[6]也对渗流问题的并行计算进行了研究。
在考虑多场耦合情况下,由于研究问题更复杂,考虑因素更多,多场耦合并行计算尚处于起步阶段,耦合问题的并行计算并不多见,而对于目前研究的热点之一——三场耦合(温度 渗流-应力耦合)问题更是如此,纵观国内外针对三场问题的研究,仅仅有 Yu-Shu Wu等[7-9]利用 TOUGH2并行版,对 Yuc-ca山中的三场试验进行了研究,并取得了不错的效果,但其他的研究成果目前尚未发现。由此本文即针对三场耦合问题,根据区域分解策略,开发三场耦合并行程序进行数值模拟,并在河海大学高性能计算机群上利用算例验证了程序的可靠性。
1 有限元并行策略
有限元并行策略主要有2种形式,一种是将大的研究域剖分为小区域,降低形成的方程组维数,即区域分解策略,另一种则是方程组解法并行策略。目前应用较多的则是2种策略方法相结合,即先进行区域分解,而后以各种预条件子的共轭梯度为解法求解。本文开发的三场耦合并行求解程序也是如此。
1.1 区域分解算法
区域分解算法[10]的基本思想是通过将一个区域划分为若干个独立的、规模较小的子区域,对一个或若干个子问题用一个处理机来处理,使原问题的求解转化为各子区域上子问题的求解,通过并行求解子问题而获得整个区域上大问题的解。区域分解算法通过对子问题的同步并行求解来缩小问题规模,降低求解复杂度,提高计算效率,体现的是“分而治之”的思想。相对于传统算法,区域分解算法的优越性体现在以下几个方面:
(1)它把大问题化为若干个小问题,缩小了计算规模;
(2)子区域形状如果规则,可以使用熟知的快速算法,如快速Fourier交换、谱方法等;
(3)允许使用局部拟一致网格,无需使用整体拟一致网格;
(4)允许不同子区域选用不同的数学模型,以便更适合于工程物理实际情况;
(5)算法高度并行,计算的主要步骤在各自子区域内独立进行。
1.2 方程组并行求解策略
方程组求解并行方面,主要是直接求解与迭代求解2种,而目前迭代法是并行求解的主流,尤其是以共轭梯度法应用为最多。本文所采用的预条件共扼梯度法[10](BICGSTAB)主要思想是基于双边Lanczos算法,收敛速度较快且平稳,许多求解器中采用的也是它。BICGSTAB算法主要计算流程如下:
(2)如果 k≤kmax且 ε≤εmax转(3),否则终止,输出→xk;

2 并行计算程序开发
2.1 编程语言
目前并行程序开发,所采用的编程语言[11]主要有MPI,OPENMP等几种,各有优略,而实际应用中MPI较多。本并行程序是利用消息传递并行编程环境MPI,结合f77实现了并行程序的开发。MPI是目前国际上最流行、可移植性和可扩展性都很好的并行程序设计环境。它是一个库,不是一门语言,可以被F77/C/F90/C++等编程语言调用,和一般的函数调用过程没什么区别,且可移植性好。
2.2 并行计算结构模式
编程模式采用主/从式(Master/Slave)结构,即并行处理由一个主进程和若干从进程组成。主进程维持全局数据结构并负责任务划分,包括接受任务,启动计算,各子进程计算任务划分及分发,回收从进程的求解结果等。而每个从进程则负责完成子任务的计算,包括局部初始化,接收主进程发来的消息;并行进行各自计算;向主进程发回各自的计算结果。它们都是操作系统的进程,在本程序中将主进程作为0号进程,而其他编号则根据主进程的任务划分确定。也就是说在整个程序中,除了求解过程各从进程之间需要进行通信外,其他的信息交换只发生在主进程和从进程之间。同时为了避免由于各进程并行读取磁盘文件所带来的复杂性,程序中所有磁盘文件的读写操作均由主进程来完成,而从进程不参与磁盘文件的读写。主从式计算的流程如图1所示。
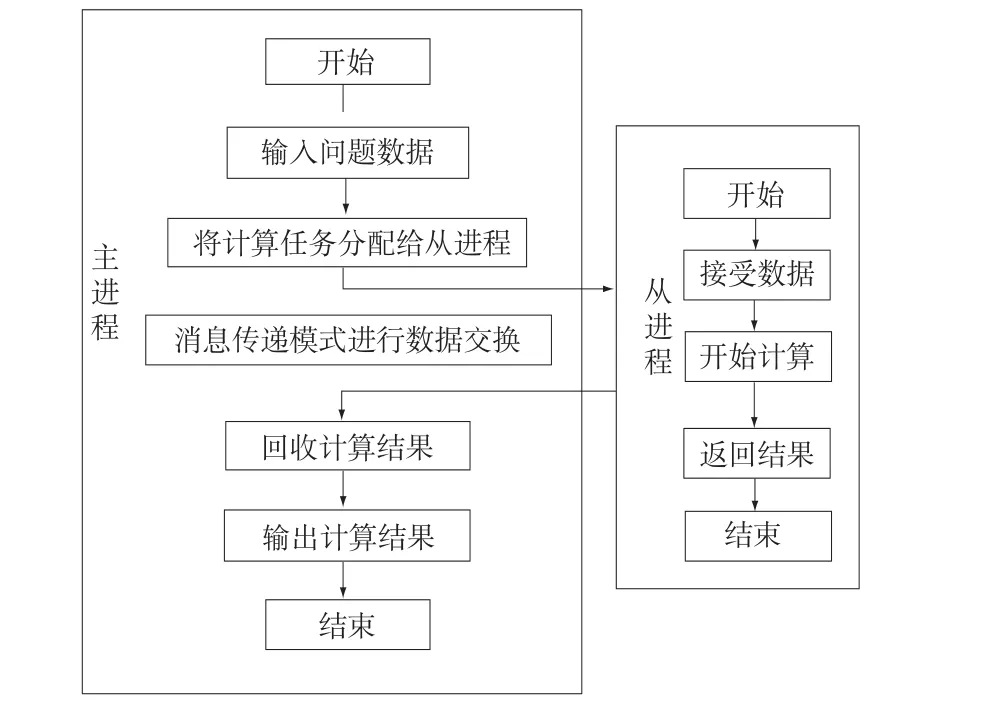
图1 主从式模型并行计算流程图Fig.1 Parallel computation flow chart in M/s model
2.3 并行计算环境
目前的并行计算环境以造价低廉的集群系统为主,许多高校、研究所等都组建了自己的集群系统进行高性能计算,所谓集群即是指通过高性能网络将一组普通微机、工作站或服务器等紧密联系在一起形成的计算机系统,每个节点都可以单独完成工作。本文所编制的计算程序即是在河海大学所组建的高性能linux计算机群上进行的调试及完成计算,该集群系统节点机配置为IBM刀片机,处理器3.2 G,内存2 G。
3 THM耦合算例验证
3.1 多孔饱和介质THM耦合方程
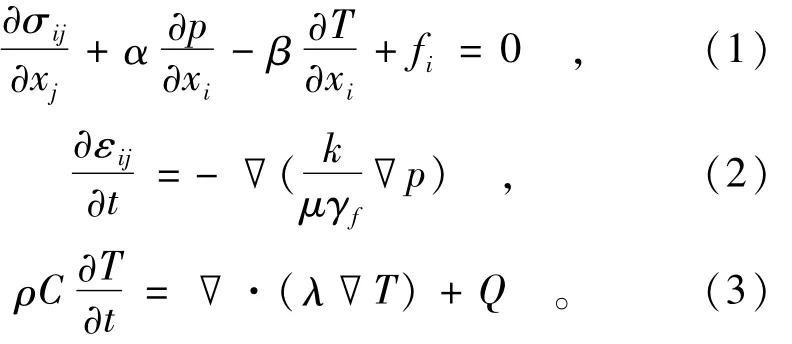
不考虑流体、固相密度随温度压力的变化,均质各向同性饱和情况下岩体的THM耦合方程如下:式中:σij为应力张量分量(i,j=1,2,3);fi为岩体介质的体积力分量,当只考虑重力时,有fi=(0,0,-ρg)T,其中ρ为岩体密度,g为重力加速度,一般取9.81 m/s2;α为 biot耦合系数;β为岩体骨架的热膨胀系数;γf为水的重度;k为渗透系数;εii=εx+εy+εz为体积变形;C为比热;λ为热传导系数;Q为热源。
对于此方程解法,串行求解一般有全耦合解法及迭代解法2种,而在并行求解过程中,考虑到计算时间,主要是采用迭代解法进行计算。本文所开发的并行程序,先计算温度场,然后计算渗流应力场,并相互迭代进行计算,而所需的参数更新可以在迭代稳定之后进行,每个时间步的迭代过程中假定参数不变。
3.2 算例验证
为对并行THM耦合计算程序的验证,构建如下算例模拟中间填埋热源、底部存在热流、上表面受均布力作用的情况,并验证并行计算效率。取研究域为110 m×50 m×90 m,域中存在两组正交裂隙,中间热源为10 m×40 m×10 m。本算例不考虑流体、固体密度随温度和压力而变的情况来进行计算,并假定代表单元体存在,根据文献[12]所提出的等效方法,将裂隙影响等效利用饱和多孔介质模型进行计算处理,即裂隙的影响可以根据应变等效、渗流量等效及热流量等效将裂隙岩体等效为饱和多孔介质进行计算。
以六面体划分单元,共划分14 560个单元,16 443个节点进行计算,自由度近8万个,研究域及网格剖分如图2所示。计算时间0~1 000 d,计算50步。边界条件与初始条件:上表面受均布力100.0 kN/m2作用,侧面法向约束,底部固定;上表面为排水边界,其他无水流量交换;上表面定温10℃,下底面有热流10.0 W/m2,中间研究区域热源20.0 W/m3。假定初始孔压为0,初温热源部分为20℃,其他为10℃。

图2 THM耦合研究域及网格剖分示意图Fig.2 THM coupling research model and FEM grids
算例所用的部分材料参数如下:岩体弹模E=60 GPa、泊松比 υ=0.23、热传导系数 λr=3.0 W/(m·℃)、热容 ρC=2.25×103kJ/(m3·℃)、线性热膨胀系数 βr=3.0×10-7(1/℃),Biot系数 α=1.0,流体的热传导系数为 λr=0.7 W/(m·℃);裂隙法向刚度、切向刚度分别为100 GPa、10 GPa,第一组裂隙隙宽30×10-6m,间距40 m,法向与z轴夹角30°,第二组隙宽20×10-6m,间距25 m,法向与z轴夹角60°,而裂隙面则都垂直于xz面。
针对本文的计算模型,先在本机上进行串行计算,然后通过将前处理模型及并行计算程序通过网页形式提交到学校IBM刀片集群系统上,分别采用4,6,8,10个节点机进行计算,具体的串并行计算时间如图3示,计算加速比及计算效率比较如图4所示。
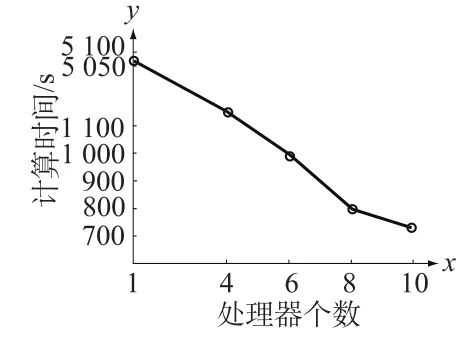
图3 THM耦合并行计算时间比较Fig.3 The comparison of computing time by different CPUs
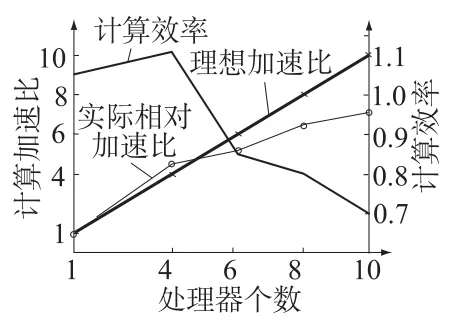
图4 THM耦合并行计算加速比及计算效率比较Fig.4 Comparison of the speedup ratio and computing efficiency by different CPUs
从图3和图4可以分析对本并行程序的计算性能:
(1)计算时间上,节点数越多所用的计算时间越少,如单机计算时间需5 069 s,并行4节点为1 146 s,6节点为997 s,而10节点则减少为724 s,另外每增加2个计算节点时,计算时间减小量越来越小,正如图3中的斜率所示;
(2)加速比上,节点数越多加速比越大,如图4中所示,4节点、6节点、10节点计算的加速比分别为4.46,5.09与7.01,相应斜率也在降低;
(3)计算效率上,如图4所反映,随节点增多计算效率越来越低,如4节点、6节点及10节点的计算效率分别为110.8%,84.9%和70.1%,参与计算的节点数越多,计算效率越低。一般情况下并行计算的实际加速效率都不会达到100%,对于4节点超过100%的情况,主要是由于个人PC与集群系统节点机的配置不同所造成的,计算个人PC配置为赛扬2.4 d,768 M内存,而集群节点机则为IBM刀片机,处理器3.2 G,内存2 G,配置相差较大也引起了较大的误差。
从加速比及计算效率上可以看出,虽然采用并行计算可以大大减少计算时间,但也并不是采用的计算节点越多越好,根据自己的计算规模采用合适的计算节点参与计算即可,以避免计算资源浪费,针对本文算例根据计算效率变化可知,采用4节点参与计算即可满足计算需求。
[1] 张友良,冯夏庭,茹忠亮.基于区域分解算法的岩土大规模高性能并行有限元系统研究[J].岩石力学与工程学报,2004,23(21):3 636-3 641.
[2] 茹忠亮,冯夏庭,张友良,等.地下工程锚固岩体有限元分析的并行计算[J].岩石力学与工程学报,2005,24(1):13-17.
[3] 刘耀儒,杨 强,黄岩松,等.基于双重孔隙介质模型的渗流-应力耦合并行数值分析[J].岩石力学与工程学报,2007,26(4):705-711.
[4] 刘耀儒,周维垣,杨 强.有限元并行EBE方法及应用[J].岩石力学与工程学报,2005,24(17):3023-3028.
[5] WANG K P,BRUCH J C.A SOR Iterative Algorithmfor the Difference and the Finite Elementmethods That is Ef-ficient and Parallelizable[J].Advances in Engineering Software,1994,21(1):37-48.
[6] 江春波,安晓谧.二维非恒定渗流的有限元并行计算[J].水科学进展,2004,15(4):454-458.
[7] WU Yu-shu,KARSTEN P.Numerical Simulation of Non-isothermal Multiphase Tracer Transport in Heterogene-ous Fractured Porous Media[J].Advances in Water Re-sources,2000,23(7):699-723.
[8] WU Yu-shu,ZHANG Keni,CHRIS D,et al.An Effi-cient Parallel-computing Method for Modeling Nonisother-mal Multiphase Flow and Multicomponent Transport in Porous and Fractured Media[J].Advances in Water Re-sources,2002,25(3):243-261.
[9] ZHANG Ke-ni,WU Yu-shu,BODVARSSON G S.Par-allel Computing Simulation of Fluid Flow in the Unsatu-rated Zone of Yucca Mountain,Nevada[J].Journal of Contaminant Hydrology,2003,62-63:381-399.
[10]胡家赣.线性代数方程组的迭代解法[M].北京:科学出版社,1997.
[11]都志辉.高性能计算并行编程技术[M].北京:清华大学出版社,2001.
[12]张强林.裂隙岩体温度渗流应力耦合数学模型研究[D].南京:河海大学,2008.
