初中数学教学中学生思维能力培养实践
2009-01-22陈金红
陈金红
数学一向被称为“思维的体操”,然而,在升学率指挥棒的指挥下,数学教学却成为了应试教学,只注重单一的知识传授,而忽视了思维品质的培养。教学中多采用表面理解、死记硬背、模仿做题的方法,其结果是培养了大批高分低能的学生,当他们遇到思维能力较强的内容时,就难以取得较好的成绩。因此,要想提高学生的学习成绩,就必须把培养学生的思维能力落实到数学教学中。
一、创设问题情景,启发学生思维
俄国心理学家鲁宾斯坦说:“思维通常是由问题的情景产生的,并且以解决问题的情景为目的。”因此,在数学课堂教学中,应该积极创设问题情景,变传授数学结论为了解知识发生发展过程的教学,使学生始终处于积极的思维之中。
1.从学生感兴趣的问题出发,创设问题情景。例如,在探究几何体表面的最短路径问题时,可设置下列问题:一只蚂蚁在圆筒外壁的A点,想吃到圆筒内壁的B点处残留的蜂蜜,怎样走路程最短?由此激发学生的求知欲望。
2.从学生的生活实际出发,创设问题情景。例如,在学习“平方根”一节时,教师提出以下问题:小明到装饰城购买瓷砖,老板给了他一块面积为4dm2的正方形瓷砖,聪明的你能告诉小明这块瓷砖的边长吗?若面积为5 dm2,则边长应为多少呢?由此,就引出了平方根的概念。
选择有意义的现实问题创设情景,更能培养学生良好的思维品质和应用意识。可见,问题是思维的灵魂,创设良好的问题情景是激发思维的有效方法。教师要善于把握学生的思维特点,在教学的重点、难点或关键处设计问题,创设问题情景,以激发学生的求知欲望,并启发学生的思维,提高学生自主解决问题的能力。
二、加强思维训练,培养思维品质
1.一题多解,拓宽思路,培养思维的广阔性。思维的广阔性是指思维发挥作用的广阔程度,它集中表现为思路宽广,能全面考察问题,用多方面的知识、经验去寻求解决问题的方法。在教学中,教师要选择典型的题目,鼓励学生积极思考,引导他们多角度、多方位、多层次地观察和思考问题,在广阔的范围内寻求解法,从而培养思维的广阔性。
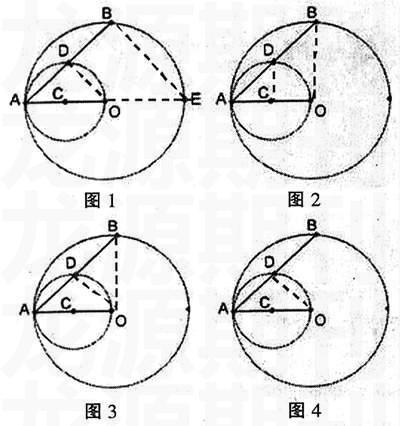
例:如图,OA是⊙o的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,求证:D是AB的中点。
证法一:如图1,延长AO交⊙O于点E,连结OD、BE,
∵ OA、EA分别是⊙C、⊙O的直径,
∴∠ADO=∠ABE=90°,OD∥EB,
又∵ OA=OE
∴ AD=BD
证法二:如图2,连结CD、OB,
∵ AC=CD,AO=BO,
∴ ∠ADC=∠A=∠B,CD∥OB,
又∵ AC=OC,
∴ AD=BD。
证法三:如图3,连结OD、OB,
∵ OA是⊙C的直径,
∴ OD⊥AB,
又∵ OA=OB,
∴ AD=BD。
证法四:如图4,连结OD,
∵ AO是⊙C的直径,
∴ OD⊥AB,AD=BD(由垂径定理)。
通过以上四种证法,从多角度、全方位去思考,去分析已知求证的关系,从而在特定的条件下培养了学生思维的广阔性。
2.一题多变,拓展延伸,培养思维的深刻性。思维的深刻性是指思维的抽象程度、逻辑水平和思维活动的深度。它集中表现为能深刻理解概念,深入思考问题,使用抽象概括,抓住事物本质,善于总结规律,并学会迁移应用。在教学中,教师要善于挖掘题目的潜在功能,恰当地进行延伸、演变、拓广,使学生的思维处于积极、兴奋的最佳状态,在疑惑、好奇的情景中,在跃跃欲试的状态下,激起思维波澜,进行思维活动,从而对问题的本质及解题规律有更深刻的理解,并培养思维的深刻性。
例:如图,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F。
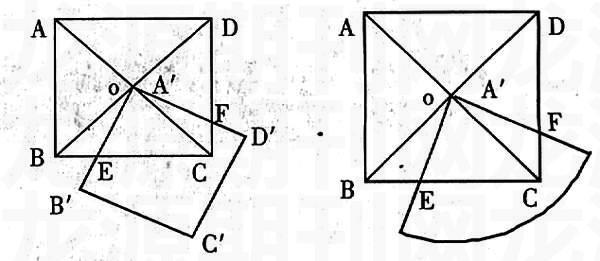
(1)若点E是BC的中点,那么F是CD的中点吗?两正方形重合部分的面积是多少?
(2)若A′B′C′D′绕点O旋转到任意位置,BE=CF 吗?重合部分的面积是多少?
(3)若将正方形A′B′C′D′换成圆心角为直角的扇形,并将它绕点O旋转,上述结论还成立吗?
本题从特殊到一般,层层深入思考,形成上述结论的实质是:两条互相垂直的直线经过正方形ABCD的对称中心,其大小以及是否是正方形都是非本质的。
3.逆向思维,培养思维的敏捷性。思维的敏捷性是指思维活动的反应速度。它集中表现为能迅速地发现、分析和处理问题,能简缩运算环节和推理过程。有些学生反应迅速,思维敏捷;有些学生反应迟钝,思维呆板;还有学生在解题中很容易生搬硬套,机械模仿,形成思维定势。因此,在教学中教师要选择一些用常规方法难以解决或解法很繁而用某种特殊方法却能迅速获解的题目来训练学生的思维,消除思维定势的影响,跳出常规解法的圈子,从而培养思维的敏捷性。
例如,计算:(1)4100×0.25100;(2)0.299 ×5101;(3)(1/8)33×299;(4)3100的末位数是几?这是一组具有启发性和技巧性的题目,正向思考,思路自然,但计算繁难,若引导学生进行反向思考,逆用幂的运算性质,则解法就会比较简捷、巧妙。
三、实施过程教学,发展思维能力
斯托利亚尔指出:“数学教学是数学活动(思维活动)的教学,而不仅是数学活动的结果——数学知识的教学。”在课堂教学中,教师要向学生提供充分从事数学活动的机会,让学生动手实践、自主探索、合作交流,积极参与知识发生、发展的过程,在这过程中促进自身思维的发展。
例如,在进行“轴对称和轴对称图形”的教学时,笔者制作了多幅轴对称图形,利用多媒体教学,展示了把一个图形沿着某一条直线折叠,与另一个图形重合的过程,同时,还让学生通过观察、体会、思考交流,得出轴对称的概念。最后,收到了较好的教学效果。
总之,培养学生的思维能力,是数学教学中一项长期而又艰苦的系统工程。在数学教学中,要重视数学思想的渗透,数学方法的训练,使学生掌握科学的思维方法,从而形成良好的思维习惯。
