基于系统动力学的短生命周期产品供应链牛鞭效应研究

汤卫克 姜大立 甘 明 黄 淞

摘要:通过因果关系分析构建了短生命周期产品供应链订货、发货子系统的系统动力学模型结构图及方程,在Vensim的模拟环境下,运行模型并对结果进行分析,提出消减牛鞭效应的对策建议。

关键词:短生命周期产品;供应链;牛鞭效应;系统动力学

中图分类号:F224文献标识码:A

Abstract: This paper uses the analysis of cause and effect way to establish Short life cycle product supply chain demand and supply systems dynamics model and equations. Run the SD model and analyses its operation and results through Vensim simulation, put forward the recommendations of the bullwhip effect reduction.

Key words: short life cycle product; supply chain; bullwhip effect; system dynamics

当今全球化市场环境中,客户需求日益呈现出不确定性、多样性和动态性,企业竞争日益激烈,产品生命周期日趋缩短。Abbas A. Kurawarwala和Hirofumi Matsuo[1]指出:短生命周期产品是指其生命周期短至几个月,最长不超过3年的一类产品,如时尚产业(如玩具、服装等)以及一些高科技产业(如计算机、电子消费类产品)等。短生命周期产品使得供应链库存控制呈现出复杂的动态行为,一定程度上增加了库存协调控制的难度,供应链失调最直接的表现就是产生牛鞭效应。

1短生命周期产品供应链系统模型的构建

系统动力学是一门以系统反馈控制理论为基础,以计算机仿真技术为主要手段,定量地研究系统发展动态行为的一门应用学科,属于系统科学的一个分支[2-3]。系统动力学自身的特性决定了系统动力学适合处理长期性和周期性的问题、对数据不足的问题进行研究、处理要求不高的复杂的社会经济问题以及处理非线性和多重反馈的复杂时变系统,能做长期的、动态的、战略性的仿真分析与研究,分析研究系统的结构与动态行为[4]。

根据系统动力学原理,对短生命周期产品供应链进行因果关系分析,消费者的需求量增加,即零售商销售量的增加,会造成零售商库存量的下降,因而又引起了零售商订货量的增加。由此可以看出消费者需求量(零售商的销售量)—零售商的库存—零售商的订货量之间负—负反馈的关系。其它各因素之间的反馈关系可依据相同的分析步骤得出。为了使总的反馈结构形成闭合回路,模型中在生产商生产量到零售商库存之间建立间接的正反馈关系。模型总的因果关系如图1所示。

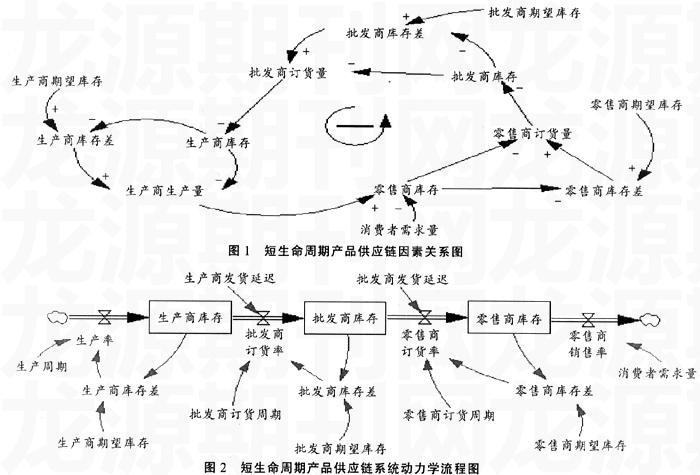
因果关系图只描述了反馈结构的基本方面,不能表示不同性质变量的区别。现由短生命周期产品供应链因果关系图画出它的系统动力学流图。如图2所示。

2模型的数据准备及运行

为了便于在以下的分析中模拟系统的行为,更好的量化牛鞭效应的程度,在此假设一个传统库存控制模式下的案例。

本文针对某一企业的生产情况进行假设。为了保证上游企业对下游需求的充分供应,假设生产商的库存≥批发商的库存

≥零售商的库存;而且通常批发商的订货周期≥零售商的订货周期。因此对该模型中主要参数做出如下的基本假设:

(1)消费者需求量:初始100件/周,10周后150件/周

(2)零售商的订货周期=0.5周

(3)零售商的库存量的初始值=150件

(4)零售商的期望库存=100件

(5)批发商的订货周期=1周

(6)批发商发货延迟时间=1周

(7)批发商的库存量的初始值=1 500件

(8)批发商的期望库存=1 000件

(9)生产商生产周期=2周

(10)生产商发货延迟时间=1.5周

(11)生产商的库存量的初始值=3 000件

(12)生产商的期望库存=2 500件

通过分析以上流程图中表示出的各个参数的相互关系,可以得出该供应链模型的基本方程如下:

(01)零售商订货率=DELAY3(零售商库存差/零售商订货周期,批发商发货延迟)

Units:件/周

(02)零售商订货周期=0.5

Units:周

(03)零售商库存=INTEG(零售商订货率—零售商销售率,150)

Units:件

(04)零售商库存差=零售商期望库存—零售商库存

Units:件

(05)零售商期望库存=100

Units:件

(06)零售商销售率=消费者需求量

Units:件/周

(07)批发商订货率=DELAY3(批发商库存差/批发商订货周期,生产商发货延迟)

Units:件/周

(08)批发商订货周期=1

Units:周

(09)批发商发货延迟=1

Units:周

(10)批发商库存=INTEG(批发商订货率—零售商订货率,1 500)

Units:件

(11)批发商库存差=批发商期望库存—批发商库存

Units:件

(12)批发商期望库存=1 000

Units:件

(13)生产率=生产商库存差/生产周期

Units:件/周

(14)生产商发货延迟=1.5

Units:周

(15)生产商库存=INTEG(生产率—批发商订货率,3 000)

Units:件

(16)生产商库存差=生产商期望库存—生产商库存

Units:件

(17)生产商期望库存=2 500

Units:件

(18)生产周期=2

Units:周

(19)FINAL TIME=30

Units:周

The final time for the simulation.

(20)INITIAL TIME=0

Units:周

The initial time for the simulation.

(21)消费者需求量=100+STEP50,10

Units:件/周

(22)SAVEPER=TIME STEP

Units:周

The frequency with which output is stored.

(23)TIME STEP=0.25

Units:周

The time step for the simulation.

短生命周期产品供应链关系模型运行如图3所示。

短生命周期产品供应链关系模型库存变化如图4所示。

3运行结果分析

从模型中库存变化图可以看出:供应链中上游企业相对于下游企业的库存量变化幅度有不同程度的增加;上游企业对下游需求量的响应也在不断的放大;同时,随着时间的推移,供应链上各节点企业的库存量也在逐渐的放大。此时整个供应链系统出现了“牛鞭效应”。

通过分析系统趋于收敛的条件,调整订货周期和发货延迟时间,对模型进行改进,可以看出改进后模型的响应是趋于稳定的收敛函数。如图5所示。

同时,通过供应链的协调,订立合理的契约,建立完善的激励机制和监督机制,实行有效的信息共享,可以减轻甚至消除牛鞭效应。在具体的运作中,可采用销售数据和库存信息共享,减少供应链环节,缩短订货的提前期或交货时间,买卖双方协调订货以及建设起战略性伙伴关系、加强各企业的合作机制等策略。

价格也是影响短生命周期产品供应链牛鞭效应的一个重要因素,在以后的研究中,将在系统动力学模型中加入价格因素,对各要素之间进行因果关系分析,深入对短生命周期产品供应链进行研究。

参考文献:

[1] A.A. Kurawarwala, H. Matsuo. Product Growth Models for Medium-Term Forecasting of Short Life Cycle Products[J]. Technological Forecasting and Social Change, 1998(57):169-196.

[2] Foresster J w. Urban Dynamics[M]. Cambridge MA: Productivity Press, 1969.

[3] Peter Senge. 第五项修炼[M]. 郭进隆,杨硕英,译. 上海:上海三联书店,1994.

[4] 苏懋康. 系统动力学原理及应用[M]. 上海:上海交通大学出版社,1988.