浅析直线度和平行度检测数据处理的教学
2009-01-12蒋兴建
【摘要】笔者针对直线度、平行度检测数据处理这一教学内容中出现的问题,围绕如何体现最小条件这一评定基本原则、区分所测数据坐标含义、明确坐标差与垂直距离的关系、如何找准基准、如何确定旋转量这五个教学关键点作了全面深刻的阐述。
【关键词】直线度;平行度;检测;数据处理
直线度、平行度是两项常用的形位公差,直线度、平行度误差的检测是《公差配合与技术测量》课程中的一项基础、重要的内容。如何处理检测得来的数据是这一教学内容的一个重点和难点。在教学中经常会碰到如下问题:
①如何在数据处理中体现最小条件?
②部分同学对所测数据的坐标含义理解不清晰。
③部分同学对图解法中采用坐标差计算最小区域法的宽度认识模糊。
④如何找准平行度误差计算中的基准?
⑤如何确定旋转法中的旋转量等。
笔者根据多年的教学实践,为解决上述问题谈点粗浅体会。
1.把握好评定形位误差的基本原则——最小条件
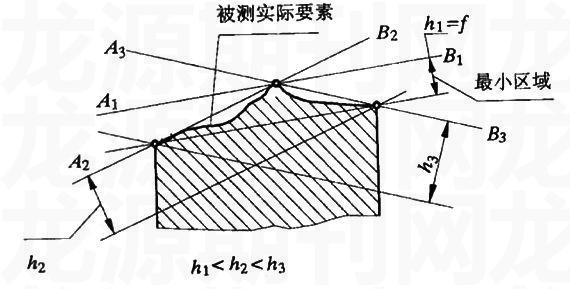
最小条件是指确定理想要素位置时,应使理想要素与实际要素接触,并使被测实际要素对其理想要素的最大变动量为最小。如下图所示,A1B1、A2B2、A3B3分别是处于不同位置时的理想要素,h1、h2、h3分别是被测实际要素对三个不同位置的理想要素的最大变动量。从图中可以看出h1 最小条件在评定形位误差中的应用——最小区域法。所谓最小区域法是指包容被测实际要素时具有最小宽度或直径的包容区域,这个包容区域是以符合最小条件的理想要素为基础建立起来的。如上图所示,我们已经分析A1B1是符合最小条件的理想要素,现作一和A1B1平行的直线,此直线和A1B1一起对被测要素形成包容,并且使此直线到A1B1的距离为最小。显然,两条平行直线所形成的对被测实际要素的包容区域为最小区域,被测实际要素在给定平面内的直线度误差值就等于此包容区域的宽度,即f= h1。 如何判断所形成的包容区域为最小区域呢?标准规定,是否为最小区域可根据与公差带形状相同的理想要素与实际被测要素的接触形式判别。例如,给定平面内直线度,由两条平行直线包容实际线段时,成高、低相间的三点接触,具有下图中(a)、(b)两种形式之一,则两平行直线就构成最小区域,这种判别准则称为相间准则。 教学中,只有把握好最小条件这一基本原则及最小条件应用中的最小区域法,才能在实际检测中将所测数据进行合理的处理,并得出客观真实的结论。 2.区分好用水平仪、百分表测量所得数据的坐标含义 水平仪和百分表是形位误差检测中的两种常用量具,都可用于测量平板或导轨在给定平面内的直线度误差情况。用水平仪测量时,沿测量长度方向分段布点依次移动,并使前一次测量的末点与后一次测量的始点重合。为此,每次测量得到的读数是相对于前一点读数的相对测量值。用百分表测量时,将被测零件用支承置于平板上,平板工作面为测量基准,按一定的布线对被测表面上各测量点进行测量。为此,每次测量得到的读数是相对测量基准的绝对测量值。在用图解法作图时,相对测量值表现为相对坐标,绝对测量值表现为绝对坐标。在用计算法处理数据时,需将相对测量值转化为绝对测量值,即将各点数据进行累加求和处理。 教学中,经常有同学对这两种量具测得读数不加区分地进行计算,出现将水平仪测量的读数当作绝对测量值或将百分表测量的读数当作相对测量值来处理的错误。只有让学生了解实测中读数的来历,即测量的方法和原理,才能真正理解所测读数是相对测量值还是绝对测量值,在处理这些数据时才不会出现上述错误。 3.理解好图解法中的坐标差与垂直距离的关系 在用图解法进行直线度或平行度误差计算时,曲线中最大误差值或格数(用水平仪测量时一般先用格数进行处理,然后再转化为误差值)的计算中,为什么采用坐标差值n,而不采用曲线偏离基准线的垂直距离n′作为直线度或平行度误差值或格数呢?如下图所示。 同学们在学习中一定会提出这个问题,只有较好地解释好这个问题,澄清模糊认识,他们才能真正掌握直线度或平行度误差检测数据处理的方法,并加以灵活运用。为此,在教学中必须引导他们理解好坐标差与垂直距离的关系。 对这个问题,我作了如下剖析:这是因为误差曲线的横坐标采用了很大的缩小比例,纵坐标采用了很大的放大比例,所以,误差曲线并不是被测要素的真实形状,真正的误差值是通过曲线上各点的坐标距离反映出来的,如果用垂直距离作为导轨直线度误差,这并不是此坐标点所对应的真正误差值。从角度这个方面理解,由于纵坐标和横坐标采用了截然不同的比例绘制,使得本来角度很小的α变大了,如上图中的α值,若水平仪的精度为0.02/1000mm,垫铁长度为250mm ,则水平仪气泡每移动一格的线性误差值为0.02/1000×250=0.005mm,曲线右端点坐标值为1.5格,即0.0075mm,那么tgα=0.0075/2000=0.00000375, α=0.75″,这样小的角度值几乎忽略不计。也就是说,由上图的A点作基准线的垂直线,若纵横坐标采用同样比例的话,实际上就是AB,即坐标差值线,而图形中的垂直线AC反而不与基准线垂直了。这就是我们在数据处理中采用坐标差的原因。 通过上述剖析,同学们透切地理解了图解法中的坐标差实际上就是垂直距离。 4.找准平行度误差计算中的理想基准要素 平行度是限制被测实际要素对基准在平行方向上变动量的一项指标,因而要得到平行度误差值,首先要确定基准。图样上标注的基准是理想基准要素,而在测量时,零件上存在的是基准实际要素。因此测量时必须要找到基准实际要素的理想要素,以此作为基准,才能评定出平行度误差的数值。怎样找准基准实际要素的理想要素可以说是教学的一个关键问题。依据标准规定,实际基准要素的理想要素的位置应符合最小条件,也就是说在确定理想要素的位置时应使实际基准要素对其理想要素的最大变动量为最小。例如实例中直线B对A的平行度误差计算中的理想基准要素就是符合最小条件的包络实际直线A的两条平行线,再作理想基准要素的平行线去包络实际被测要素直线B,形成与理想基准要素平行的最小包容区域,此最小区域的宽度就是所测实际要素的平行度误差值。可以说,只要找准了平行度误差计算中的理想基准要素,平行度误差值的计算问题就迎刃而解了。 5.确定好旋转法中的旋转方向和旋转量 旋转法在直线度误差检测中实际上就是将被测实际要素按理想要素状态进行旋转调平,而理想要素状态必须符合最小条件。为此,旋转调平的目的就是将按最小区域法包络实际要素的两条平行的包络线(理想要素状态)处于水平位置,这时被测实际要素就符合相间准则,最高点最低点的差值就是被测要素的直线度误差值。 在数据处理中,旋转量多少全凭各人的经验,经常会碰到要进行多次旋转处理,才能使所测数据符合相间准则。怎样在旋转法中用一种比较科学的方法,较明确地确定旋转量和旋转方向,使得计算一步到位呢?在教学中这样提出问题,解决问题,不仅提高了课堂教学效果,而且培养了学生的思维能力和解决问题的能力。具体的方法是:先要分析清楚被测实际要素的高低情形,初步确定旋转调平后最低点、最高点的位置,使哪两个最低点值相等或哪两个最高点值相等。


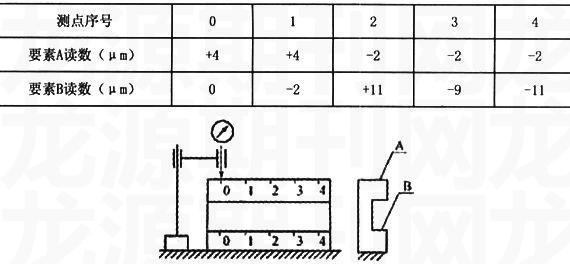



例如实例中直线A的直线度误差计算中,根据各测点读数值可知:要调平,工件右端需向上抬高(旋转方向);并可初步判定测点1和4为最高点,测点2为最低点。设测点1绕测点0向上旋转量为p,则其它测点的旋转量如下表:
要使两最高点的值相等,即+4+p=-2+4p,可解得p=2。
同样,实例中直线B的直线度误差计算中,旋转方向:右端向上抬高;测点0和3为最低点,测点2为最高点。设测点1绕测点0向上旋转量为q,则其它测点的旋转量如下表:
要使两最低点的值相等,即0=-9+3q,得q=3。
通过上述分析和计算可快捷地确定旋转法中的旋转方向和旋转量。既“少走了弯路”(避免了反复旋转寻找符合相间准则的情形),又“授之以渔”(教给了学生一种探究问题的方法)。
实例:
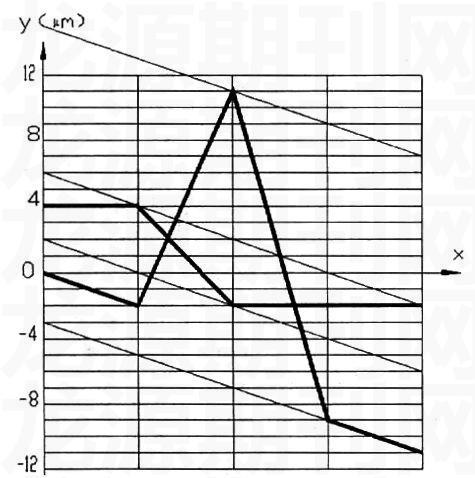
如图所示,用打表法沿恒定方向测量实际直线A和B,各点读数如下表所列。用最小区域法求出A和B的直线度误差值。假定A、B同在垂直于测量平板的某一平面内,A为基准要素,B为关联被测要素,求B对A的平行度误差值。
解法一:图解法
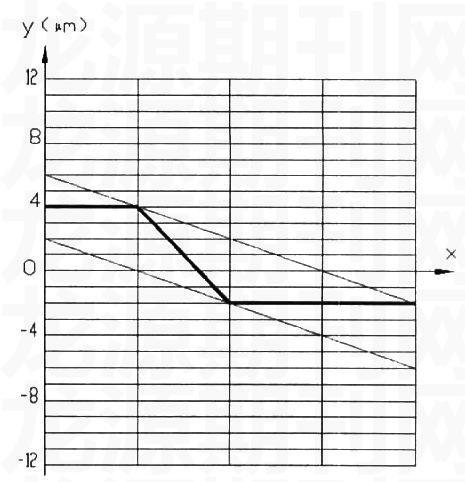
(1)直线A的直线度误差曲线如下图所示:
作出直线A的符合最小区域法的两条平行的包络线,两条包络线坐标差为4μm。
即A的直线度误差值为4μm。
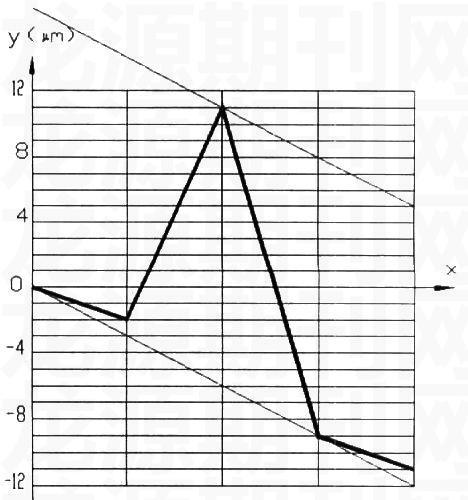
(2)直线B的直线度误差曲线如下图所示:
作出直线B的符合最小区域法的两条平行的包络线,两条包络线坐标差为17μm。
即B的直线度误差值为17μm。
(3)直线B对A的平行度误差曲线如下图所示:
因A为基准要素,B为关联被测要素,故以直线A的两条平行的包络线(直线A的理想要素)作为平行度测量基准要素,去作直线B的两条包络线,两条平行的包络线坐标差为18μm。
即直线B对A的平行度误差值为18μm。
解法二:旋转法
(1)直线A的直线度误差:
符合“高(0)——低(-4)——高(0)”相间准则的评定原则。
直线A的直线度误差值为4μm。
(2)直线B的直线度误差:
符合“低(0)——高(+17)——低(0)”相间准则的评定原则。
直线B的直线度误差值为17μm。
(3)直线B对A的平行度误差:
因A为基准要素,在直线A的直线度计算中,右端向上旋转2(μm)。为此,我们以此旋转后的数值作为A的理想要素(基准要素),要素A、B的右端同时向上旋转2(μm)后的数值为:
直线B对A的平行度误差为+15-(-3)=18μm。
对比两种解法,可以看出:图解法直观形象地体现了最小区域法,而旋转法通过两端位置的上下调整体现了相间准则。两种解法的结果是一致的,也进一步佐证了图解法中的坐标差实际上就是垂直距离这一结论。
通过以上实例两种方法的讲解后,同学们对直线度、平行度检测数据处理这一教学内容不仅容易接受,而且感受较深,并能透彻理解和掌握所学知识,收到了很好的教学效果,为其它项目的形位公差检测数据处理打下了坚实的基础。
参考文献
[1]公差配合与技术测量[M].中国劳动社会保障出版社,2000.
[2]极限配合与技术测量习题册[M].中国劳动社会保障出版社,2007.
[3]刘巽尔.几何量公差[M].北京理工大学出版社,1992.
作者简介:蒋兴建(1965—),湖南潇湘技师学院机械专业高级讲师,从事《公差配合与技术测量》等机械类技术基础课程教学二十余年。
