浅谈初中数学教学中创造性思维的培养

　　在研究性学习过程中，鼓励教师在教学中“要提倡灵活多样的教学方式，尤其是采用启发式和讨论式的设问，充分发展学生的个性，发展其思维能力，激发想象力和创造潜能”，“避免烦琐的分析和琐碎机械的练习”。可见，灵活巧妙的设问，不仅具有活跃课堂气氛的功能，更具有培养学生创造性思维的作用。
　　
　　一、创设良好的课堂情境。激发创造精神
　　
　　我国的传统教育比较注重学生求同思维的养成，往往容易忽视对学生求异品质的塑造。因此，我们在课堂教学中，应充分利用一切可供想象的空间，充分发挥学生的想象力，培养学生的创造力。
　　要创设合适的问题情境，激发学生探讨数学问题的兴趣。学习兴趣和求知欲是学生能否积极思维的动力。在数学问题情境中，新知识的需要与学生原有的数学水平之间存在着认识冲突，而这种冲突正是诱发学生数学思维的积极性和创造性所必需的。
　　例如：对于分式a+2/a²4a+4-6-b/b²-8b+12的化简，就可设计如下的诱发过程以引导学生：
　　大多数学生对分式的加减运算都懂得先通分后加减，但这一方法对本题不适用，教师可问学生能否用其他方法对它进行化简。譬如，分别观察分式的分子、分母，寻找形式上的特点。通过教师这一引导性的提问激发起了学生的兴趣，学生的思维便活跃起来，积极对该式进行观察、分析。原来：a²+4a+4可化为(a+2)²；b²=-8b+12可化为(b-6)·(b-2)。从而达到了化简的目的。
　　
　　二、教师启发要与学生的思维同步
　　
　　教师提出问题后，一般应让学生先作一番思考，必要时教师可作适当的启发引导。教师的启发要遵循学生思维的规律，因势利导，循序渐进，不能强制学生按照教师提出的方法和途径去思考问题，喧宾夺主。例如：初中学生在学习“三角形相似的判定”这一内容时，教师可选用如下的例题。
　　
　　例：已知：如图1，△ABC中，BE和CF是中线，它们相交于点G，
　　求证：FG·CG=EG·BG
　　如果有的教师没有认真揣摩学生的思路，径直提出连结EF，强行让学生证明△E-FG≌BCG。那么就可能脱离学生的实际，没能与学生的思维同步。有经验的教师往往“既备教材，又备学生”，在备课时认真揣摩学生的心理，估计课堂上可能发生的各种情况。对于这道例题，学生可能会去证明ABGF和△CGE相似，教师应让学生多讨论，去发现这两个三角形不一定相似，即使相似，也不符合本题结论的要求。如此一来，就为学生滤去了疑惑。此时学生不须再启发，也会利用“点E、F分别为边AC、AB的中点”这一条件，进而联想到连结EF。
　　
　　三、要不断向学生提出新的教学问题
　　
　　问题不仅是教学的心脏、教学思维的动力，更是思维的方向。数学思维的过程就是不断地提出问题和解决问题的过程。因此，在数学课堂教学中，教师要及时地向学生提出新的数学问题，为更深入的数学思维活动提供动力和方向，使数学思维活动持续不断地向前发展。提出适当的数学问题必须符合下列条件；
　　
　　①问题要有方向性。
　　②问题的难度要适中。
　　③问题要有启发性。
　　有的教师往往把启发式误认为提问式，认为问题提得越多越好。其实，问题并不在多，而在于是否具有启发性、是否是关键性的问题、是否能触及问题的本质，引导学生深入思考。
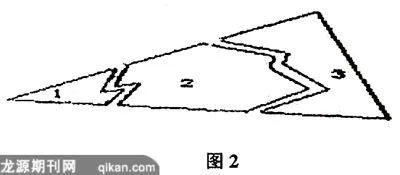
　　如图2，用一块打破成三块的三角形玻璃引入全等三角形的判定时，教师问：“若带碎片1去，带去了三角形的几个元素?若带碎片2去，带去了三角形的几个元素?若带碎片3去，带去了三角形的几个元素?”这就是个极为关键、富有启发性的问题，它引起了学生浓厚的兴趣，带动学生深入思考，并为学生学习应和“角边角公理”奠定了基础。
　　
　　(责任编辑：张华