多边形重点讲练
2008-06-06陈德前
陈德前江苏省数学特级教师,江苏省兴化市教育局教研室副主任,中国管理科学研究院学术委员会特约研究员,江苏省考试研究会会员,江苏省教育学会中学数学教育专业委员会会员,泰州市教育学会数学教育委员会会员,兴化市人民政府兼职督学,兴化市数理化学会会员,兴化市教育学会副秘书长.
一、正多边形的概念
1. 概念
各条边相等,各个内角也相等的多边形叫做正多边形.
2. 理解正多边形需要注意的两点
(1)边数为n(n > 3)的多边形,必须同时满足“各条边相等”、“各个内角相等”两个条件,我们才能说它是正多边形.如菱形的各条边相等,但各个内角不一定都相等,它不一定是正四边形(即正方形).又如矩形的各个内角相等,但各条边不一定相等,所以它不一定是正四边形(即正方形).
(2)当多边形的边数为3时,只要满足“各条边相等”、“各个内角相等”两个条件中的任意一个,它就是正三角形,这是一个特例.
3. 例题赏析
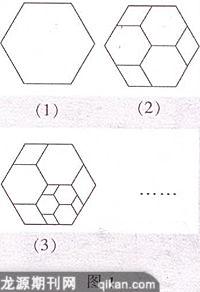
例1(2007年河南中考题)将图1(1)所示的正六边形进行分割得到图1(2),再将图1(2)中某一个较小的正六边形按同样的方式进行分割得到图1(3), 再将图1(3)中某一个较小的正六边形按同样的方式进行分割……则在第n个图形中共有个正六边形.
[解析:]该题主要是对正六边形进行分割.图1(1)中有1个正六边形,即3×(1-1)+1=1;图1(2)中有4 个正六边形,比图1(1)中多 3个正六边形,即3×(2-1) +1=4;图1(3)中有7个正六边形,比图1(2)中多3个正六边形,即3×(3-1)+1=7……所以第n个图形中正六边形的个数为3(n-1)+ 1=3n-2.
二、正多边形的镶嵌
1. 对镶嵌的理解
正多边形能否镶嵌成平面图案,关键是看这些正多边形位于同一个重合的顶点周围的内角之和是否等于360°.
2. 例题赏析
例2(2007年长沙市中考题)单独使用正三角形、正方形、正六边形、正八边形4种地砖中的某一种,不能密铺地面的是.
[解析:]正三角形的每个内角都是60°,360°÷60°=6,用6个正三角形就可以密铺地面.正方形的每个内角都是90°,360°÷90°=4,用4个正方形就可以密铺地面.正六边形的每个内角都是120°,360°÷120°=3,用3个正六边形就可以密铺地面.正八边形的每个内角都是135°,360°÷135°的结果不是正整数,所以用正八边形不可以密铺地面.
例3(2006年武汉市中考题)阳光中学阅览室正在装修,装修工人准备用边长相等的正方形地砖和正三角形地砖密铺地面.每个重合的顶点周围的正方形地砖、正三角形地砖的块数分别是().
A. 2、2 B. 2、3C. 1、2D. 2、1
[解析:]正方形的每个内角都是90°,正三角形的每个内角都是60°,2×90°+3×60°=360°.应选B.
三、即学即练
1. 一个多边形的内角和为720°,则这个多边形的边数为___________.
2. (2006年云南中考题)正多边形的一个外角为 36°,则这个正多边形的边数为().
A. 6B. 8C. 10D. 12
3. (2007年哈尔滨市中考题)哈尔滨市进行城区人行道翻新,准备选用同一种正多边形地砖铺设地面.下列正多边形地砖中,不能进行平面镶嵌的是().
A. 正三角形 B. 正方形
C. 正五边形 D. 正六边形
参考答案:1. 62. C3. C
