有效“数学化”应注意的问题

　　数学教学是一种活动，这种活动是学生经历“数学化”过程的活动，是学生基于经验基础上的自主建构数学知识的活动。因而《数学课程标准》在关于课程目标的阐述中，首次大量使用了“经历、感受、体验、体会、探索”等刻画数学活动水平的过程性目标动词，这充分表明学生是“数学化”的主体，教师要努力让学生经历有效的“数学化”过程。
　　
　　一、活动——弗牵
　　
　　让学生亲身经历以探究为主的学习活动是有效数学化的主要途径，活动有效，“数学化”才会有效。《数学课程标准》在“基本理念”中也强调：“教师应激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能，数学思想与方法，获得广泛的数学活动经验。”在活动中，教师要注重引导，而不是牵着学生鼻子走，让学生只做活动的执行者，更不能为了赶时间，而使活动过程有形无质。
　　如很多老师在教“平行四边形的面积”时，都是先让学生把一个平行四边形沿高剪开后转化成长方形，然后让学生比较平行四边形的底与长方形的长、平行四边形的高与长方形的宽之间的关系，在着重强调转化前后的图形面积不变的基础上，使学生得出“平行四边形的面积：底×高”的结论。虽然课堂上小手如林、小嘴常开，但整个活动过程，学生的思维含量低，学生只是充当了按教师指令亦步亦趋完成任务的操作工。教师的教是高效的，学生的学却不是很有效。所以学生在后面遇到这样的练习(国标苏教版五年级上册第14页)：“用细木条钉成一个长方形框，长12厘米，宽7厘米。它的周长和面积各是多少?如果把它拉成一个平行四边形，它的周长变化了没有?面积呢?你能说说这是为什么吗?”
　　
　　有近半数学生这样回答：它的周长变了，面积没有变，因为平行四边形转变成长方形后面积不变。这充分暴露了学生活动中按教师指令操作探究的弊端。
　　在教学中，教师要努力变“程式化”的训练为引导学生有效亲历“数学化”活动的过程。如上述案例中，教师事先可以给每个学生提供一张统一大小的平行四边形纸片，让学生自主量出需要的数据，自主探究出这个平行四边形的面积。操作方法让学生自己想，活动方案由学生自己设计，老师只是以合作者、引导者的身份参与到学生的活动中。在学生得出平行四边形的面积后，让学生展示自己的思考过程、操作过程。这里面必定有对有错，再让学生在讨论交流的过程中明辨是非，从而让学生真正经历有效的“数学化”活动的过程。
　　
　　二、体验——弗抑
　　
　　体验是个性化的，它不可替代、不可传递。正如荷兰数学家弗赖登塔尔所言，数学学习是一种数学化活动的过程，这种活动过程与游泳、骑自行车一样不经过亲身体验，仅仅从看书本、听讲解、观察他人的演示是学不会的。所以教师不可以强迫学生接受某个概念，因为，学生如果缺乏相关的体验支撑，这个概念在学生的头脑中始终是模糊不清、难以正确建立的。
　　开学初，听一位年轻老师给一年级学生上《比一比》，比较轻重时，教师先出示挂图，告诉学生图上画的是天平，并进一步指出：天平可以用来比较物品的轻重，当天平两边的物品一样重时天平两边就一样高，也就是天平平衡，如果天平两边的物品不一样重，天平就不平衡，重的一边会往下沉。然后让学生看天平图比较石榴和柿子的轻重，学生根据天平图示很快判断出是柿子重。老师很高兴，接着让学生看下面的两幅图比较其中物品的轻重：
　　
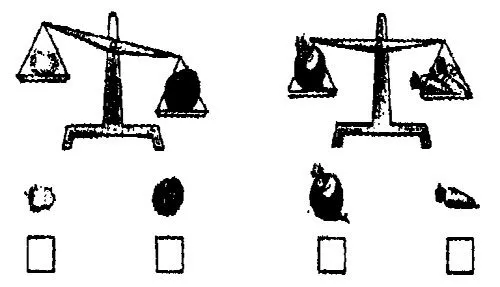
　　第一幅图学生没有争议，都认为是西红柿比辣椒重。但第二幅图问题就来了，有的说：一样重!因为天平是平衡的!有的喊：红萝卜重!因为红萝卜大!有的叫：胡萝卜重!因为胡萝卜长!教师让学生讨论了半天，最终还是没有结果。这时老师追问：一个红萝卜和三个胡萝卜一样重，一个红萝卜不是比一个胡萝卜重吗?老师这样强调了好几遍，直到下课铃声响起的时候，一个学生还喊：“胡萝卜重!”令这位年轻的老师哭笑不得。可见，强迫的“数学化”过程是没有效果的。教师以自己的体验替代了学生的体验，学生比较时只会机械地看“天平”。最后一题，图中的天平是平衡的，目的是让学生进行简单的推理，让学生进行数学思考，提升学生思维的含量。但学生缺乏应有的体验，将物品的轻、重与物品的大、小或长、短相混，头脑中一点轻重的概念都没有，怎么能根据“1个红萝卜和3根胡萝卜同样重”的图示，推理得出“1个红萝卜比1根胡萝卜重的结论”呢?因此。笔者认为，教师应将实物天平带进课堂，在比较物品的轻重时，先让学生用手掂一掂，后勉励学生说一说掂的感受，再引导学生将物品放用天平上比一比，勉励学生说出用天平比的结果，让学生有效体验比较的过程。再有意识让学生比一比一只大气球和一个小皮球的轻重、一枝长铅笔和一个小魔方的轻重，使学生正确建立关于轻重的概念。
　　马芯兰教师曾经说过：“儿童的智慧在自己的指尖上。”的确，学生在动手操作体验的过程中，能够获得直接经验和亲身体验，能有效地促进学生对数学的理解，从而有效完成“数学化”的过程。
　　
　　三、建构——弗达
　　
　　《数学课程标准》指出：教师应“从学生已有的生活经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程。”在数学课堂教学中，学生建构数学知识的过程是师生双方交互作用的历程。教师是组织者和引导者，而非“讲题者”；学生是主动探索知识的“建构者”，而非只是一个“模仿者”。数学课堂“生活化”也不是最终目的，只是有效“数学化”的途径。所以，教师要引导学生打开思路，而不能给学生提供现成的答案，要把注意力放在引导学生进行有效构建和再创造的过程之中。如，下图是国标苏教版四年级下册《找规律》中的生活场景图：
　　
　　目的是让学生联系生活实际问题理解“选配”的含义，学习不重复、不遗漏的有序选配，探索计算选配方案总个数的方法。教学时可以让学生经历以下几个层次，进行有效建构。
　　第一层次：让学生用实物摆一摆，记录下自己所发现的选配方案。
　　这一层次是实物操作，开始学生的操作可能是无序的，但是在操作的过程中，为了不重复、不遗漏，无序就会渐变成有序。在交流时可以引导学生有序汇报：如选第一顶帽子有哪几种选配的方案?选第二顶呢?如果选第一个木偶娃娃，有哪几种选配方案?选第二个呢?选第三个呢?教师可以根据学生的汇报依次用图片再现学生的选配方案。使操作行为在学生头脑中留下具体生动、条理分明的印象。
　　第二层次：用下面不同颜色的三角形和不同颜色的梯形分别表示两顶不同的帽子和三个不同的木偶娃娃，用连线的方法找出所有选配方案。
　　
　　这一层次是图形操作，用图形代替实物，用连线表示选配，再次体会选配的过程和策略，这个层次的活动目的是引导学生进行深入的数学思考。数学教学中的解决实际问题，其目的不应局限于问题的答案是什么，教学的价值更体现在获得实际问题里的数学知识和数学思想方法。
　　第三层次：引导学生抽象出用算式2×3(或3×2)算出所有选配方案的方法，并能结合第一层次和第二层次来解释其中的算理。这一层次是符号操作，让学生在头脑里再现选配操作活动的全过程，反思在图形间连